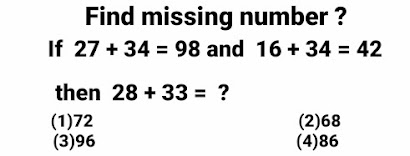Ten Missing number questions with solutions for ssc cgl exam
Ten Missing number questions with solutions for ssc cgl exam are discussed in this post . These questions of reasoning in latest reasoning questions with answers are very very important for upcoming competitive exams like Bank PO , SSC CGL etc . So let us start solving and understanding these Maths logical reasoning questions with answers.
Problem # 1
 |
| Exam Cracker |
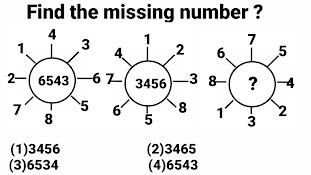
Problem # 2
 |
| Exam Cracker |
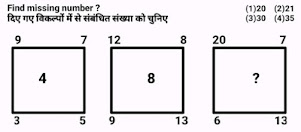
Problem # 3
 |
| Exam Cracker |
Formula :- Sum of squares of four numbers around the circle is = Middle number
Problem # 4
 |
| Exam Cracker |
Problem # 5
 |
| Exam Cracker |
Problem # 6
 |
| Exam Cracker |
Problem # 7
 |
| Exam Cracker |
Problem # 8
 |
| Exam Cracker |
Problem # 9
Problem # 10
 |
| Exam Cracker |