Ten most expected missing number series questions for SBI PO with solution for other competitive Exams
Missing number series questions for SBI PO with solution
Problem # 1
49 - 16 = 33 (The difference of 2nd and 3rd number is pair of odd number three )
104 - 49 = 55 (The difference of 3rd and 4th number is pair of odd number five)
? - 104 = 77 ( Similarly the difference of 4th and 5th number will pair of odd number seven)
⇒ ? = 77 + 104 (And in the same way the difference of 5th and 6th number is pair of odd number nine )
⇒ ? = 181
280 - ? = 99
⇒ ? = 280 - 99
⇒? = 181
Option (2)181 will be correct option
Problem # 2
Problem # 3
In this series every number is written as power of one greater than the term,s position and taking as base of 5 . i.e. 1st term is written as power of 0 , 2nd term is written as power of 1, 3rd term is written as power of 2 , 4th term is written as power of 3 and so on.5⁰ + 0 = 1 + 0 = 1 (Power 0 of base 5 + same power )
5¹ + 1 = 5 + 1 = 6 (Power 1 of base 5 + same power )
5² + 2 = 25 + 2 = 27 (Power 2 of base 5 + same power )
5³ + 3 = 125 + 3 = 128 (Power 3 of base 5 + same power )
5⁴ + 4 = 625 + 4 = 629 (Power 4 of base 5 + same power )
5¹ + 1 = 5 + 1 = 6 (Power 1 of base 5 + same power )
5² + 2 = 25 + 2 = 27 (Power 2 of base 5 + same power )
5³ + 3 = 125 + 3 = 128 (Power 3 of base 5 + same power )
5⁴ + 4 = 625 + 4 = 629 (Power 4 of base 5 + same power )
Problem # 4
In this series every number is written as cube of the term,s position and one number less than it . i.e. 1st term is written as cube of 1 and less than 1 , 2nd term is written as cube of 2 and less than 1, 3rd term is written as cube of 3 and one lees than it , 4t term is written as cube of 4 and one less than it and so on.
Problem # 5
(5 × 1) + 2 = 5 + 2 = 7 ( To get 2nd term Multiplying 1st term with 1 and add 2 to it)
Problem # 6
Problem # 7
Problem # 8
2 .Box and circle reasoning
3 . Reasoning for bank exams
4. Ten Tricky logical reasoning
5. Missing number series questions
6. Reasoning questions with answers
7. Circle Reasoning
8. Box Problems
9. 15 Questions Circle Problems
10. SSC CGL Reasoning
Problem # 9
To get 3rd term from 2nd term we just multiplied it with double of the number what we have multiplied in last term i.e. 2 × ( 1/2) =1
6 × 1 = 6
To get 4th term from 3rd term we just multiplied it with double of the number what we have multiplied in last term i.e. 2 × ( 1) =2
6 × 2 = 12
To get 5th term from 3rd term we just multiplied it with double of the number what we have multiplied in last term i.e. 2 × ( 2 ) =4
12 × 4 = 48
To get 6th term from 5th term we just multiplied it with double of the number what we have multiplied in last term i.e. 2 × ( 4 ) =8
48 × 8 = 384
Hence (2)384 will be correct option
Also Reads these posts on Reasoning
ReasoningProblems #11
ReasoningAnalogy #10
Reasoning Questions #9
Circle Reasoning #8
TenBox-Problems #7
TenReasoning problems #6
Ten-Important-Problem#5
Ten--Tricky-Puzzles #4
Twelve-Figures-Problems#3
Ten-Important-Reasoning#2
Picture-Reasoning#1
Ten most important Missing number series questions and answers, Number Series Questions for SBI Clerk ,SBI PO with solution for SSC GL , SSC CHSL , RRB NTPC and other competitive Exams were discussed in this post. comment your valuable suggestions regarding this post and for further improvement.


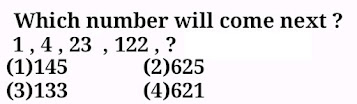















No comments:
Post a Comment
Your valuable suggestions are always acceptable to us for betterment of this website