15 Most Important Questions of Reasoning in Circle Problems
15 Missing term in circle reasoning with solution have been discussed in this post . These types of problems are very helpful for cracking competitive exams like ssc cgl, ssc chsl , RRB NTPC, Group D and various Bank exams and many other similar exams.
15 Most Important circle Problems of Reasoning for different competitive Exams
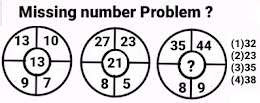
Problem # 1
Add all the numbers in every circle except middle number then divide it with 3 to get middle number.
{ 13 + 10 + 7 + 9 } / 3 = 39 / 3 = 13 ( Middle number in 1st picture)
{ 27 + 23 + 5 + 8 } / 3 = 63 / 3 = 21 ( Middle number in 2nd picture)
{ 35 + 44 + 9 + 8 } / 3 = 96 / 3 = 32 ( Middle number in 3rd picture)
Hence option (1) is right answer.
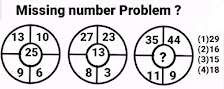
Problem # 2
Multiply both the numbers in the second line then divide it with difference of the numbers in the 1st line of every figure. In last step add "7" to it to get the number in the middle of every figure.
{ ( 9 * 6 ) / ( 13 -10 ) } + 7 = ( 54 / 3 ) + 7 = 18 + 7 = 25 ( Middle number in 1st picture )
{ ( 8 * 3 ) / ( 27 - 23) } + 7 = ( 24 / 4 ) + 7 = 6 + 7 = 13 ( Middle number in 2nd picture )
{ ( 11 * 9 ) / ( 44 - 35 ) } + 7 = ( 99 / 9 ) + 7 = 11 + 7 = 18 ( Middle number in 3rd picture ).
Hence option (4) is right answer.
Problem # 3
This figure consist of four sectors and every sector consists of three numbers. Every number in the inner part of each sector is H C F ( Highest Common Factor ) of two other numbers, which are in outer part of each sector.
HCF of 12 and 27 = 3HCF of 16 and 24 = 8
HCF of 2 and 3 = 1
Similarly HCF of 4 and 8 = 4 ( The value of question mark )Hence option (1) is right answer.
Problem # 4
This figure consist of four sectors and every sector consists of three numbers. Every number in the inner part of each sector is HCF ( Highest Common Factor ) of two other numbers which are in outer part of each sector.
H C F of 12 and 15 = 3
H C F of 6 and 4 = 2
H C F of 3 and 2 = 1
H C F of 12 and 6 = 6 ( The value of question mark)
Hence option (4) is right answer.
Problem # 5
This figure consist of four sectors and every sector consists of three numbers. Every number in the inner part is LCM ( Lowest Common Multiple ) of two other numbers which are in outer part of each sector.LCM of 12 and 15 = 60 LCM of 9 and 6 = 18LCM of 3 and 2 = 6 LCM of 8 and 6 = 24 (The value of question mark)Hence option (4) is right answer.
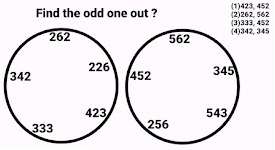
Problem # 6
All the Numbers except one in both the circles are written in same pattern . If we multiply all the three digits of any number in both the circles then we shall get same result except in one number in both the circles. And that different result will be the odd one out in this problem.
In 1st circle
The product of digits of number 262 = 2 * 6 * 2 = 24
The product of digits of number 226 = 2 * 2 * 6 = 24
The product of digits of number 423 = 4 * 2 * 3 = 24
The product of digits of number 333 = 3 * 3 * 3 = 27 ( Odd one out)
The product of digits of number 342 = 3 * 4 * 2 = 24
In 2nd circle
The product of digits of number 562 = 5 * 6 * 2 = 60
The product of digits of number 345 = 3 * 4 * 5 = 60
The product of digits of number 543 = 5 * 4 * 3 = 60
The product of digits of number 256 = 2 * 5 * 6 = 60
The product of digits of number 452 = 4 * 5 * 2 = 40 ( Odd one out)
So from both these circles two results 27 and 40 of numbers 333 and 452 are different from other.
Hence option (3) is right answer.
Problem # 7
All the Numbers except one in both the circles are written in same pattern . If we add all the three digits of any number in both the circles then we shall get same result except in one number in both the circles. And that different result will be the odd one out in this problem.
In 1st circle
The sum of digits of number 163 = 1+ 6 + 3 = 10
The sum of digits of number 145 = 1 + 4 + 5 = 10
The sum of digits of number 334 = 3 + 3 + 4 = 10
The sum of digits of number 441 = 4 + 4 + 1 = 9 ( Odd one out)
The sum of digits of number 343 = 3 + 4 + 3 = 10
In 2nd circle
The sum of digits of number 414 = 4 + 1 + 4 = 9
The sum of digits of number 333 = 3 + 3 + 3 = 9
The sum of digits of number 444 = 4 + 4 + 4 = 12 ( Odd one out).
The sum of digits of number 504 = 5 + 0 + 4 = 9
The sum of digits of number 108 = 1 + 0 + 8 = 9
So from both these circles two results 9 and 12 of numbers 441 and 444 are different from other.
Hence option (2) is correct answer.
Problem # 8
In this circle all the numbers are written in a line and the sum of each line is 25. Starting from the line which is right side of ? ( Question mark),
4 + 11 + 3 + 7 = 25
10 + 1 + 9 + 5 = 25
11 + 6 + 2 + 6 = 25
? + 5 + 5 + 8 = 25
⇒ ? + 18 = 25
? = 25 - 18 = 7
Hence option (1) is correct answer
Also read these posts on Reasoning
Problem # 9
Here 1st circle consist of four numbers and if we divide sum of all the digits in its outer part with total numbers then result will be the middle number.
( 3 + 8 + 7 + 2 )/4 = 20/4 = 5 ( Middle number)
2nd circle consist of five numbers and if we divide sum of all the digits in its outer part with total numbers then result will be the middle number.
( 6 + 4 + 8 + 5 + 7 )/5 = 30/5 =6 ( Middle number)
3rd circle consist of six numbers and if we divide sum of all the digits in its outer part with total numbers then result will be the middle number.
( 9 + 7 + 8 + 9 + 7 + 8 )/6 = 48/6 =8 ( Middle number)
Hence option (2) is correct answer
Problem # 10
This figure consist of four sectors and every sector consists of three numbers. Every number in the inner part is cube of difference of two other numbers which are in outer part of each sector. ( 8 - 5 )³ = 3³ = 27 ( 23 - 19 )³ = 4³ = 64 ( 3 - 2 )³ = 1³ = 1 (26 - 24)³ = 2³ = 8 ( The value of question mark)Hence option (4) is correct answer
Problem # 11
This figure consist of four sectors and every sector consists of three numbers. Every number in the inner part is Four times of square of difference of two other numbers which are in outer part of each sector.4 × (11 - 8)² = 4 × (3)² = 4 × 9 = 36 4 × (5 - 5)² = 4 × (0)² = 4 × 0 = 0 4 × (7 - 3)² = 4 × (4)² = 4 × 16 = 64 4 × (8 - 2)² = 4 × (6)² = 4 × 36 = 144 ( The value of question mark)Hence option (1) is correct answer
Problem # 12
This figure consist of four sectors and every sector consists of three numbers. Every number in the inner part is cube of difference of two other numbers which are in outer part of each sector. (11 - 8)³ = 3³ = 27 (5 - 4)³ = 1³ = 1(7 - 3)³ = 4³ = 64 (8 - 2)³ = 6³ = 216 ( The value of question mark)Hence option (1) is correct answer
Problem # 13
This figure consist of four sectors and every sector consists of three numbers. Every number in the inner part is five times of product of two other numbers which are in outer part of each sector.
( 6 × 3 ) × 5 = 18 × 5 = 90( 2 × 3 ) × 5 = 6 × 5 = 30
( 4 × 2 ) × 5 = 8 × 5 = 40
( 5 × 4 ) × 5 = 20 × 5 = 100 ( The value of question marks ) .
Hence option (1) is right answer.
Problem # 14
This figure consist of four sectors and every sector consists of three numbers. Every number in the inner part is the sum of two other numbers which are in outer part of opposite sector to these numbers.
24 + 11 = 35 ( The number opposite to both 24 and 11 ) . 13 + 26 = 39 ( The number opposite to both 246and 13 ) .
9 + 25 = 34 ( The number opposite to both 9 and 25 ) .
7 + ? = 35 ( The number opposite to both 7 and ? ) .
So if we put ? = 28 then we shall have total equal to 35.
Hence option (2) is right answer
Problem # 15
All the Numbers except one in both the circles are written in same pattern . If we multiply all the three digits of any number in both the circles then we shall get same result except in one number in both the circles. And that different result will be the odd one out in this problem.
In 1st circle
The product of digits of number 145 = 1 * 4 * 5 = 20
The product of digits of number 451 = 4 * 5 * 1 = 20
The product of digits of number 225 = 2 * 2 * 5 = 20
The product of digits of number 541 = 5 * 4 * 1 = 20
The product of digits of number 255 = 2 * 5 * 5 = 50 (Odd one out)
In 2nd circle
The product of digits of number 414 = 4 * 1 * 4 = 16
The product of digits of number 444 = 4 * 4 * 4 = 64 (Odd one out)
The product of digits of number 224 = 2 * 2 * 4 = 16
The product of digits of number 441 = 4 * 4 * 1 = 16
The product of digits of number 128 = 1 * 2 * 8 = 16
So from both these circles two results 50 and 64 of numbers 255 and 444 are different from other.
Hence option (3) is right answer.




















No comments:
Post a Comment
Your valuable suggestions are always acceptable to us for betterment of this website