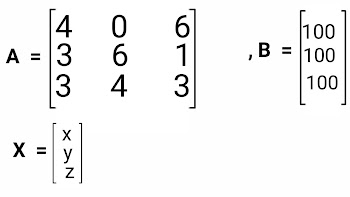
Simplest and shortest Matrix method to solve linear equations of 3 variables
Matrix method to solve linear equations of 3 variables
In this post we are going to understand the concept of solving linear equations of three variables with the help of matrix method .
Matrix method to solve linear equations of three variables with the help of example.