Ten Most Important Reasoning Problems of Circles with Solutions, How to Solve Reasoning Circle Problems
Ten Most Important Reasoning problems of circles with solutions. These types of problems are very helpful for cracking competitive exams like ssc cgl, ssc chsl and various Bank exams and many other similar exams .
Ten Most Important Reasoning Problems of Circles with Solutions.
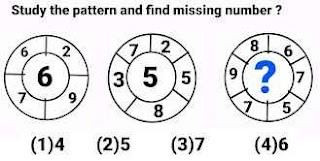
Problem # 1
1st circle
2nd circle
3rd circle
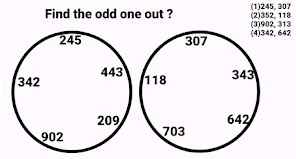
Problem # 2
This circle consists of four quadrants and every quadrant consists of three numbers , And every quadrant have two numbers in outer part and 1 number in the inner part . To find the value of question mark "?" , we shall use two numbers which are in the outer part to calculate the value of the number which is in the inner part of every quadrant .
1st Quadrant
8² × 3⁴ = 64 × 81 = 5184
Now add all these digits 5 + 1 + 8 + 4 = 18
Now reversing the order of these digits obtained in previous step
18 <----> 81 The number in the inner part
2nd Quadrant
Now add all these digits 6 + 0 + 0 + 2 + 5 = 13
Now reversing the order of these digits obtained in previous step
13 <----> 31 The number in the inner part
4th Quadrant
8² × 9⁴ = 64 × 6561 = 419904
Now add all these digits 4 + 1 + 9 + 9 + 0 + 4 = 27
Now reversing the order of these digits obtained in previous step
27 <----> 72 The number in the inner part
3rd Quadrant
7² × 7⁴ = 49 × 2401 = 117649
Now add all these digits 1 + 1 + 7 + 6 + 4 + 9 = 28
Now reversing the order of these digits obtained in previous step
28 <----> 82 The number in the inner part
Option (1) is correct option.
Problem # 3
This circle has been divided into eight sectors. Every sector consist of three numbers. To solve this problem multiply both the numbers in any sector which are in the outer part and then add 1 to it ,the result so obtained is written in the inner part of the sector which is exactly opposite to this sector .Continuing in this manner we shall have all the numbers placed accordingly. . Starting from the sector immediately to the right of question mark.
( 2 × 4 ) + 1 = 9 ( In the inner part of 5th sector )
( 3 × 7 ) + 1 = 22 ( In the inner part of 6th sector )
( 1 × 6 ) + 1 = 7 ( In the inner part of 7th sector )
( 5 × 2 ) + 1 = 11 ( In the inner part of 8th sector )
( 3 × 4 ) + 1 = 13 ( In the inner part of 1st sector )
( 2 × 9 ) + 1 = 19 ( In the inner part of 2nd sector )
( 2 × 2 ) + 1 = 5 ( In the inner part of 3rd sector )
( ? × 3 ) + 1 = 25 ( In the inner part of 4th sector )
Now we have to find the value of "?" like this
( ? × 3 ) + 1 = 25
? × 3 = 25 - 1
? × 3 = 24
? = 24/3
? = 8
Hence option (2) is correct option.
Problem # 4
1st Sector
2nd Sector
3rd Sector
4th Sector
Problem # 5
In 1st circle
In 2nd circle
Problem # 6
1st Quadrants
2nd Quadrants
3rd Quadrants
4th Quadrants
Problem # 7
Problem # 8
Problem # 9
2 .Box and circle reasoning
3 . Reasoning for bank exams
4. Ten Tricky logical reasoning
5. Missing number series questions
6. Reasoning questions with answers
7. Circle Reasoning
8. Box Problems
9. 15 Questions Circle Problems
10. SSC CGL Reasoning
Problem # 10
In 1st Sector
In 2nd Sector
In 3rd Sector
In 4th Sector
Also Reads these posts on Reasoning
Reasoning Problems #11
Reasoning Analogy #10
Reasoning Questions #9
Circle Reasoning #8
Ten Box-Problems #7
Ten Reasoning problems #6
Ten-Important-Problem#5
Ten--Tricky-Puzzles #4
Twelve-Figures-Problems#3
Ten-Important-Reasoning#2
Picture-Reasoning#1
















No comments:
Post a Comment
Your valuable suggestions are always acceptable to us for betterment of this website