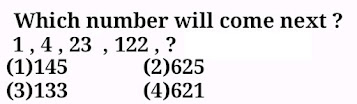Ten Tricky logical reasoning questions+answers , Latest reasoning questions with answers

No comments

Ten latest and Tricky logical reasoning questions+answers are discussed in this post . These questions of reasoning in latest reasoning questions with answers are very very important for upcomig competitive exams like Bank PO , SSC CGL etc . So let us start solving and understanding these Maths logical reasoning questions with answers.

Problem #1

Ten Tricky logical reasoning questions+answers

Magnitude of {(7 + 5) (7 - 5 ) - cube of 5 } = 125 - 12 *2 = 125 - 24 = 101

Magnitude of {(8 + 3) ( 8 - 3 ) - cube of 3 } = 11 * 5 - 27 = 55 - 27 = 28

Magnitude of {(6 + 2) ( 6 - 2 ) - cube of 2 } = 8 * 4 - 8 = 32 - 8 = 24

Magnitude of {(5 + 4) ( 5 - 4 ) - cube of 4 } = 64 - 9*1 = 64 - 9 = 55

Note :- Magnitude of difference of two numbers means , we have to consider the difference of two numbers irrespective of their positions, And the magnitude of difference of two numbers will always be a positive value .The magnitude of 3 - 2 and 2 - 3 will be same and will be equal to 1 ( not -1) and magnitude of 7 - 9 and 9 - 7 will be same and equal to 2 ( not -2 ), Similarly the magnitude of 11 - 2 and 2 - 11 will same and equal to 9 ( not -9 ).

Alternate Method

Magnitude { {7² - 5² } - ( 5³ ) } = ( 5³ ) - {7² - 5² } = 125 - ( 49 - 25) =125 - 24 = 101

Magnitude { {8² - 3² } - ( 3³ ) } = {8² - 3² } - ( 3³ ) = ( 64 - 9 ) - 27 = 55 - 27 = 24

Magnitude { {6² - 2² } - ( 2³ ) } = {6² - 2² } - ( 2³ ) = ( 36 - 4) - 8 = 32 - 8 = 24

Magnitude { {5² - 4² } - ( 4³ ) } = ( 4³ ) - {5² - 4² } = 64 - ( 25 - 16 ) = 64 - 9 = 55

Option (2) is correct

Problem #2

Difference of both the digits of numbers in outer circle of any Quadrant - (difference of digits of numbers in inner circle of any Quadrant ) = two in every case

(55 - 52 ) - (9 - 8) = 3 - 1 = 2

(29 - 21 ) - (9 - 3) = 8 - 6 = 2

(18 - 12) - (8 - 4) = 6 - 4 = 2

(7 - 5) - (4 - 4) = 2 - 0 =2

Option (4) is correct

Problem #3

1st quadrant

4 × (7 - 3)² = 4 × 4² = 4 × 16 = 64

2nd quadrant

4 × (5 - 5)² = 4 × 0² = 4 × 0 = 0

3rd quadrant

4 × (11 - 8)² = 4 × 3² = 4 × 9 = 36

4th quadrant

4 × (8 - 2)² = 4 × 6² = 4× 36 = 144

Option (3) is correct option

Problem #4

In this figure the sum of the digits of the numbers obtained from the multiplication of both the numbers which are outer part of that particular quadrant.

8 × 2 = 16 = 1 + 6 = 7 digit in middle left box

6 × 5 = 30 = 3 + 0 = 3 digit in middle left box

6 × 9 = 54 = 5 + 4 = 9 digit in middle right box

4 × 1 = 04 = 0 + 4 = 4 digit in middle right box

Option (2) is correct option

Problem #5

(11 - 7 )³ = 4³ = 64 (1st number in 2nd row )

(14 - 11 )³ = 3³ = 27 ( 2nd number in 2nd row )

(64 - ?)² = 4³ = 8 ( It will be 3rd number in 2nd row )

So ? = 66

Alternate Method

Add the cube root of respective number in 2nd row to the number in 1st row to get number in 3rd row.

7 + 64⅓ = 7 + 4 = 11 ( 1st number in 3rd row)

11 + 27⅓ = 11 + 3 = 14 ( 2nd number in 3rd row)

64 + 8⅓ = 64 + 2 = 66 ( 3rd number in 3rd row)

Option (B) is correct option

Problem #6

Pick all prime number up to 11

1st prime number = 2

Multiply it with next number

2 × 3 = 6 ( 2nd number in the series)

2nd prime number = 3

Multiply it with next number

3 × 4 = 12 ( 3rd number in the series)

3rd prime number = 5

Multiply it with next number

5 × 6 = 30 ( 4th number in the series)

4th prime number = 7

Multiply it with next number

7 × 8 = 56 ( 5th number in the series)

5th prime number = 11

Multiply it with next number

11 × 12 = 132 ( 6th number in the series)

Option (D) is correct option

Problem #7

Add the twice of the number in 1st column to the half of the number in 2nd column to get the 3rd number in every row.

( 2 × 6 ) + ( 8 ÷ 2 ) = 12 + 4 = 16 ( 1st number in 3rd column)

( 2 × 1 ) + ( 6 ÷ 2 ) = 2 + 3 = 5 ( 2nd number in 3rd column)

( 2 × 3 ) + ( 10 ÷ 2 ) = 6 + 5 = 11 ( 3rd number in 3rd column)

Option (A) is correct option

Problem #8

Divide with 10 the Multiplication/Product of all the numbers which are in the outer part of triangles to get the number in the centre of the triangle. And this method will be applicable to all the three triangles.

1st triangle

(5 × 6 × 4 ) ÷ 10 = 120 ÷10 =12

2nd triangle

(6 × 7 × 5 ) ÷ 10 = 210 ÷10 =21

3rd triangle

(4 × 8 × 10 ) ÷ 10 = 320 ÷10 =32

Option (3) is correct option

Problem #9

Here every figure consist of three numbers in 1st line and one number in 2nd line. And 2nd number written in every figure is the (HCF) Highest common Factor of all the three numbers in the 1st line in each figure.

H C F ( Highest common Factor ) of 9 ,15 , 18 = 3 (1st figure )

HCF ( Highest common Factor ) of 16 ,28 , 32 = 4 ( 2nd figure )

HCF ( Highest common Factor ) of 24 ,36 , 48 = 12 (3rd figure )

Therefore option (4) is correct option .

Problem #10

Take reverse of sum of both the numbers in every quadrant to get the number attached to middle of this figure.

9 + 8 = 17 ↔️71 ( The number in the middle of 4th Quadrant)

8 + 3 = 11 ↔️11 ( The number in the middle of 1st Quadrant)

5 + 7 = 12 ↔️21 ( The number in the middle of 2nd Quadrant)

7 + 7 = 14 ↔️41 ( The number in the middle of 3rd Quadrant)

Therefore option (2) is correct option .

In this post I discussed Ten Tricky logical reasoning questions+answers , Latest reasoning questions with answers . Comment your valuable suggestion for further improvement.

Also Read these posts on Reasoning

ReasoningProblems #11

ReasoningAnalogy #10

Reasoning Questions #9
Circle Reasoning #8
TenBox-Problems #7
TenReasoning problems #6
Ten-Important-Problem#5
Ten--Tricky-Puzzles #4
Twelve-Figures-Problems#3
Ten-Important-Reasoning#2
Picture-Reasoning#1

Ten most expected missing number series questions for SBI PO with solution for other competitive Exams

No comments

Maths Reasoning

Missing number series questions for SBI PO with solution

Ten most expected missing number series questions for SBI PO with solution , for SSC GL , SSC CHSL , RRB NTPC and other competitive Exams have been discussed in this post. These types of series questions are asked in many other competitive exams like SI, CPO and various entrance exams.

Problem # 1

Take the difference of two consecutive terms of the given series. This difference will be the pair of same odd numbers in every case.

16 - 5 = 11 (The difference of 1st and 2nd number is pair of odd number one)
49 - 16 = 33  (The difference of 2nd and 3rd number is pair of odd number three )
104 - 49 = 55  (The difference of 3rd and 4th number is pair of odd number five)
? - 104 = 77   ( Similarly the difference of 4th and 5th number will pair of odd number seven)
⇒ ? = 77 + 104  (And in the same way the difference of 5th and 6th number is pair of odd number nine )
⇒ ? = 181
280 - ? = 99
⇒ ? = 280 - 99
⇒? = 181

Option (2)181 will be correct option

Problem # 2

In this series every number is written as power of one less than the term,s position and taking as base of 5 . i.e. 1st term is written as power of 0 , 2nd term is written as power of 1, 3rd term is written as power of 2 , 4th term is written as power of 3 and so on.

5⁰ - 0 = 1 - 0 = 1 (Power 0 of base 5 - same power )

5¹ - 1 = 5 - 1 = 4 (Power 1 of base 5 - same power )

5² - 2 = 25 - 2 = 23 (Power 2 of base 5 - same power )

5³ - 3 = 125 - 3 = 123 (Power 3 of base 5 - same power )

5⁴ - 4 = 625 - 4 = 621 (Power 4 of base 5 - same power )

Option (4)621 is correct option

Problem # 3

In this series every number is written as power of one greater than the term,s position and taking as base of 5 . i.e. 1st term is written as power of 0 , 2nd term is written as power of 1, 3rd term is written as power of 2 , 4th term is written as power of 3 and so on.
5⁰ + 0 = 1 + 0 = 1 (Power 0 of base 5 + same power )
5¹ + 1 = 5 + 1 = 6   (Power 1 of base 5 + same power   )
5² + 2 = 25 + 2 = 27   (Power 2 of base 5 + same power  )
5³ + 3 = 125 + 3 = 128   (Power 3 of base 5 + same power )
5⁴ + 4 = 625 + 4 = 629   (Power 4 of base 5 + same power  )

Option (2)629 will be correct option.

Problem # 4

In this series every number is written as cube of the term,s position and one number less than it . i.e. 1st term is written as cube of 1 and less than 1 , 2nd term is written as cube of 2 and less than 1, 3rd term is written as cube of 3 and one lees than it , 4t term is written as cube of 4 and one less than it and so on.

1³ - 1 = 1 - 1 = 0

2³ - 1 = 8 - 1 = 7

3³ - 1 = 27 - 1 = 26

4³ - 1 = 64 - 1 = 62

5³ - 1 = 125 - 1 = 124

6³ - 1 = 216 - 1 = 215

Option (1)124 will be correct option.

Problem # 5

(5 × 1) + 2 = 5 + 2 = 7 ( To get 2nd term Multiplying 1st term with 1 and add 2 to it)

(7 × 2) - 4 = 14 - 4 = 10 ( To get 3rd term Multiplying 2nd term with 2 and subtract 4 to it ).

(10 × 3) + 6 = 30 + 6 = 36 ( To get 4th term Multiplying 3rd term with 4 and add 6 to it)

(36 × 4) - 8 = 144 - 8 = 136 ( To get 5th term Multiplying 2nd term with 2 and subtract 4 to it )

(136 × 5) + 10 = 680 +10= 690 ( To get 2nd term Multiplying 1st term with 1 and add 2 to it)

Option (2)690 will be correct option.

Problem # 6

To get 2nd term ,multiply 1st term with half and add cube of 1 to it .

(12 × 0.5 ) + 1 = 6 + 1 = 6 + 1³ = 6 + 1 = 7

To get 3rd term ,multiply 2nd term with one ( double of half ) and add cube of 2 to it .

(7 × 1) + 8 = 7 + 2³ = 7 + 8 = 15

To get 4th term ,multiply 3rd term with 2 ( double of 1 ) and add cube of 3 to it .

(15 × 2) + 27 = 30 + 3³ = 57

To get 5th term ,multiply 4th term with 4 ( double of 2 ) and add cube of 4 to it .

( 57 × 4 ) + 64 = 228 + 4³ = 292

To get 6th term ,multiply 5th term with 8 ( double of 4 ) and add cube of 3 to it .

( 292 × 8 ) + 125 = 2336 + 125 = 2461

option (4)2461 is correct option

Problem # 7

Multiply 1st term of the series with one and half (1.5) to get 2nd term of the series.

10 × 1.5 = 15

Multiply 2nd term of the series with 3 ( double the 1.5 i.e. 2 × 1.5 = 3 ) to get 3rd term of the series.

15 × 3 = 45

Multiply 3rd term of the series with 6 ( double the 3 i.e. 3 × 2 = 6) to get 4th term of the series.

45 × 6 = 270

Multiply 4th term of the series with 12 ( double the 6 i.e. 6 × 2 = 12 ) to get 5th term of the series.

270 × 12 = 3240

Multiply 5th term of the series with 24 ( double the 12 i.e. 12 × 2 = 24 ) to get 2nd term of the series.

3240 × 24 = 77760

Option (2)77760 is correct option

Problem # 8

(2 × 5) - 1 = 10 - 1 = 9 ( 2nd term is written as multiple of 5 with 1st term and decrease it by 1 )

(9 × 5) + 3 = 45 + 3 = 48 ( 3rd term is written as multiple of 5 with 2nd term and increase it by 3)

(48 × 5) - 5 = 240 - 5 =235 ( 4th term is written as multiple of 5 with 3rd term and decrease it by 5)

( 235 × 5 ) + 7 = 1185 + 7 = 1182 ( 5th term is written as multiple of 5 with 4th term and decrease it by 7 )

Note carefully in this problem ,operation of decreasing and increasing used alternatively.

Option (2)1182 is correct option

Problem # 9

In this series 1st term is 12 , To get 2nd term from it we just multiplied it with half

12 × 1/2 = 6

To get 3rd term from 2nd term we just multiplied it with double of the number what we have multiplied in last term i.e. 2 × ( 1/2) =1
6 × 1 = 6
To get 4th term from 3rd term we just multiplied it with double of the number what we have multiplied in last term i.e. 2 × ( 1) =2
6 × 2 = 12
To get 5th term from 3rd term we just multiplied it with double of the number what we have multiplied in last term i.e. 2 × ( 2 ) =4
12 × 4 = 48
To get 6th term from 5th term we just multiplied it with double of the number what we have multiplied in last term i.e. 2 × ( 4 ) =8
48 × 8 = 384
Hence (2)384 will be correct option

Problem # 10

To find out the solution of above series problem just add all the digits of the every number given , this sum will leads to the next number of the series

5 + 3 + 4 + 2 = 14 ( 2nd number in series)

Similarly add all the digits of the 3rd number, this sum will leads to the 4th number of the series

5 + 2 + 3 + 1 = 11 ( 4th number in series)

4 + 1 + 2 + 0 = 17 ( 6th number in series)

6 + 7 + 3 + 2 = 18 ( last/ Missing number in series)

Option (4)18 is correct option

Also Reads these posts on Reasoning
ReasoningProblems #11
ReasoningAnalogy #10
Reasoning Questions #9
Circle Reasoning #8
TenBox-Problems #7
TenReasoning problems #6
Ten-Important-Problem#5
Ten--Tricky-Puzzles #4
Twelve-Figures-Problems#3
Ten-Important-Reasoning#2
Picture-Reasoning#1

Ten most important Missing number series questions and answers, Number Series Questions for SBI Clerk ,SBI PO with solution for SSC GL , SSC CHSL , RRB NTPC and other competitive Exams were discussed in this post. comment your valuable suggestions regarding this post and for further improvement.

Ten Most Important Reasoning questions with answers for competitive exams

No comments

Maths Reasoning

Ten Most Important Reasoning questions with answers for competitive exams of circles,box and other type with solutions will be discussed in this post . These types of problems are very helpful for cracking competitive exams like ssc cgl, ssc chsl and various Bank exams and many other similar exams .

Problem # 1

Exam cracker

Divide with 2 the sum of 1st and 3rd number in every column of each row to get the number middle row .

( 7 + 9 )/2 = 16/2 = 8

(4 + 6) /2 = 10/2 = 5

(1 + ? )/2 = 2

⇒ (1 + ? ) = 4

⇒ ? = 4 - 1

⇒ ? = 3

Therefore option (B) is correct option

Problem # 2

Here every figure consist of three numbers in 1st line and one number in 2nd line. And 2nd number written in every figure is the (HCF) highest common factor of all the three numbers in the 1st line .

H C F ( Highest Common Factor ) of 4 ,8 , 12 = 4 (1st figure )

H C F ( Highest Common Factor ) of 12 ,24 , 30 = 6 ( 2nd figure )

H C F ( Highest Common Factor ) of 21 ,14 , 42 = 7 (3rd figure )

Therefore option (1) is correct option

Problem # 3

One tenth of sum of all the numbers except middle number in each box is equal to middle number in that box.

(3 * 4 * 2 * 5 )/10 = 120 / 10 = 12 ( Middle number in 1st box )

(6 * 2 * 3 * 5 )/10 = 180 / 10 = 18 ( Middle number in 2nd box )

(2 * 2 * 9 * 5 )/10 = 180 / 10 = 18 ( Middle number in 3rd box )

Therefore option (2) is correct option.

Problem # 4

Sum of the product of both the numbers in 1st and 2nd line is equal to middle numbers in each figure.

(5 * 4 ) + ( 3 * 1) = 20 + 3 = 23 ( Middle number in 1st figure )

(7 * 6 ) + ( 3 * 4) = 42 + 12 = 54 ( Middle number in 2nd figure )

(11 * 2 ) + (? * 9) = 22 + 9? = 40

⇒ 9? = 40 - 22

⇒ 9? = 18

⇒ ? = 2 ( Middle number in 3rd figure )

Therefore option (C) is correct option

Problem # 5

This problem have three figures and every figure consist of one number in the middle of the figure and four numbers around it .The product of middle number's digits is equal to the sum of the remaining numbers/digits around the figure.

7 + 4 + 7 + 12 = 30 = 5 * 6 = Product of middle number 56 in 1st figure.

15 + 7 + 12 + 8 = 42 = 6 *7 = Product of middle number 67 in 2nd figure

11 + 18 + 5 + ? = 36 = 6 * 6 = Product of middle number 66 in 3rd figure

⇒ 34 + ? = 36

⇒ ? = 36 - 34

⇒ ? = 2

Therefore option (1) is correct option

Problem # 6

This circle consists of four quadrants and every quadrant consists of three numbers , Every quadrant have two numbers in outer part and one number in its inner part . To find the value of question mark "?" , we shall use two numbers which are in the outer part of it to calculate the value of the number which is in the inner part of every quadrant .

4th Quadrant

( 7 × 4 )/4 = 28/4 = 7 ( Middle number in inner part)

3rd Quadrant

( 8 × 5 )/4 = 40/4 = 10 ( Middle number in inner part)

2nd Quadrant

( 4 × 20 )/4 = 80/4 = 20 ( Middle number in inner part)

1st Quadrant

( 6 × 8 )/4 = 48/4 = 12 ( Middle number in inner part)

Therefore option (4) is correct option

ReasoningProblems #11 ReasoningAnalogy #10

Reasoning Questions #9 Circle Reasoning #8

TenBox-Problems #7 TenReasoning problems #6

Ten-Important-Problem#5 Ten--Tricky-Puzzles #4

Twelve-Figures-Problems#3 Ten-Important-Reasoning#2

Picture-Reasoning#1

Problem # 7

This problem have three figures and every figure consist of three numbers in 1st line and one number in 2nd line. And 2nd number written in every figure is the (HCF) highest common factor of all the three numbers in the 1st line.

H C F ( Highest Common Factor ) of 12 ,18 , 30 = 6 (1st figure )

H C F ( Highest Common Factor ) of 16 ,32 , 40 = 8 (2nd figure )

H C F ( Highest Common Factor ) of 36 ,18 , 27 = 9 ( 3rd figure )

Therefore option (3) is correct option.

Problem # 8

Starting from 2 and moving clockwise multiplying two opposite numbers which will contribute 56 in each case.

2 * 28 = 56

14 * 4 = 56

Similarly the product of 7 and ? must be equal to 56.

7 * ? = 56

⇒ ? = 56/7 = 8

Therefore option (A) is correct option.

Problem # 9

This problem consist of three figures and every figure have three numbers out of which two numbers are smallest than 3rd number. So starting from smallest number and proceeding anticlockwise likewise.

Sq of 2 + Sq of 4 = 4 + 16 = 20 ( 1st figure)

Sq of 3 + Sq of 9 = 9 + 81 = 90 (2nd figure)

Sq of 1 + Sq of 5 = 1 + 25 = 26 (3rd figure)

Therefore option (3) is correct option.

Problem # 10

This circle have following numbers in it. 40 , 45, 25 , 40 , 30, 35 , 35 , ? .

Now after carefully studying these numbers, we find that these numbers are written in two alternate series . So starting from number 25 clockwise pick alternate numbers..

Our 1st pattern from these numbers 40 , 45 , 25 , 40 , 30, 35 , 35 , ? will be 25, 30 , 35 , 40 and these numbers are written with an increment of 5 . It means that the difference/increment between two consecutive numbers is same

25 + 5 = 30

30 + 5 = 35

35 + 5 = 40

After eliminating above numbers remaining numbers are 45 , 40 , 35 , ? .

Now note the difference between every two consecutive numbers is 5.

45 - 40 = 5

40 - 35 = 5

So 35 - ? = 5

⇒ -? = 5 - 35

⇒ -? = -30

⇒? = 30

Therefore option (1) is correct option .

Ten Most Important Reasoning questions with answers for competitive exams of circles, box and other type with solutions discussed in this post . These types of problems are very helpful for cracking competitive exams like ssc cgl, ssc chsl and various Bank exams and many other similar exams .

Problem #1

Problem #2

Problem #3

Problem #4

Problem #5

Problem #6

Problem #7

Problem #8

Problem #9

Problem #10

Missing number series questions for SBI PO with solution

Problem # 1

Problem # 2

Problem # 3

Problem # 4

Problem # 5

Problem # 6

Problem # 7

Problem # 8

Problem # 9

Problem # 10

Problem # 1

Problem # 2

Problem # 3

Problem # 4

Problem # 5

Problem # 6

4th Quadrant

3rd Quadrant

2nd Quadrant

1st Quadrant

Therefore option (4) is correct option

Problem # 7

Problem # 8

Problem # 9

Problem # 10

Recent Posts

My Popular Posts