Twelve Important Tricky Reasonining Problems for SSC CGL ,SSC CHSL And RRB NTPC Exams
12 Most important problems of tricky reasoning problems which includes box problems , triangles problems and star problems for competitive exams like SSC CGL ,SSC CHSL and RRB NTPC etc have been included in this post.
12 Important Tricky Reasoning Problems for Reasoning Various Exams
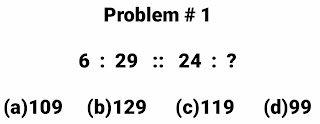
Problem # 1
Adding all the numbers which are forming triangle in corner like this
Top Right corner
10 + 13 + 9 = 32 Top Right corner
Top Left corner
15 + 10 + 7 = 32 Top left corner
Bottom Left corner
7 + 17 + 8 = 32 Bottom left corner
Bottom Right corner
Similarly 8 + 9 + ? = 32 means Question mark "?" will take the value 15. So
Option (1) is correct Option.
Problem # 2
Add all the numbers from corner which are forming rhombus and square respectively , because sum of all the numbers in both rhombus and square in corner position are equal to 34.
Rhombus
7 + 10 + 9 + 8 = 34
Square
15 + 5 + ? + 6 = 34 .
26 + ? = 34
? = 34 - 26
? = 8
This means question mark ? will have 8 value.
So Option (2) is correct Option.
Problem # 3
Add all the three numbers in every small square then divide this sum with the fourth number in same square to get result every time 10.
Top Left Square
( 9 + 4 + 7 )/2 = 20 /2 = 10
Top Right Square
( 9 + 13 + 8 )/3 = 30 /3 = 10
Bottom Left Square
( 9 + 16 + 15 )/4 = 40/4 = 10
Similarly in
Bottom Right Square
(6 + ? +3 )/1 = 10/1 = 10. If we take the value of question mark "?" equal to 1 then we shall get total equal to 10 ,
Hence Option (1) is correct Option.
Problem # 4
In all the picture add both the numbers in 1st row and then umbers in 2nd row and left number in last row, then take the difference of these sum to get the number in right side of 3rd row.
In 1st row 9 + 8 = 17, 4 + 9 = 13 then 17 - 13 = 4
In 2nd row 11 + 5 = 16 , 10 + 3 = 13 then 16 - 13 = 3 , Similarly
in 3rd row 7 + 16 = 23 , 6 + 12 = 18 then 23 - 18 = 5 .
Hence option (1) is correct option.
Problem # 5
There are five squares in this picture. To solve this problem or to find the value of question mark , sum of all the numbers in each square when divided by the number in the corner must be equal to 6 in each four figure. In the
Top Left square
( 3 + 2 + 7 ) /2 = 12/2 = 6
Top Right square
( 9 + 5 + 4) /3 = 20/3 = 6
Bottom Left square
( 9 + 7 + 8 )/4 = 24/4 = 6
Bottom Right square
( 3 + ? + 1 )/1 = (4 + ?)/1= 6.
4 + ? = 6
? = 6 - 4
? = 2
This means if we put ? = 2, Only then we shall 6 as answer.
Hence option (3) is correct option.
Problem # 6
To solve this problem divide each number in the second row with 6 , then subtract one from the answer so obtained to get the number in 1st row.
(78/6) -1 => 13 - 1 = 12 ( The 1st number in the 1st row)
(60/6 ) -1 => 10 - 1 = 9 ( The 2nd number in the 1st row)
(24/6) -1 => 4 - 1 = 3 ( The 3rd number in the 1st row)
( ?/6 - 1 ) -1 = >10 ( The 4th number in the 1st row). that is if we put ? = 66 then upon dividing 66 with 6 we shall get 11, And after subtracting 11 from 1 , we shall get the answer.
Hence option (C) is correct option.
Problem # 7
Take the square root of difference of 21 and 12 to get middle number 3. Similarly take the square root of difference of 15 and 6 to get middle number 3 in 1st picture.
Similarly take the square root of difference of 29 and 4 to get middle number 5. Similarly take the square root of difference of 36 and ? to get middle number 5 in 2nd picture.
In 1st picture
√(21 - 12 ) = √9 = 3
√(15 - 6 ) = √9 = 3
In 2nd picture
√(29 - 4 ) = √25 = 5
√(36 - ? ) = √25 = 5 , If we put ? = 11 then we can solve this problem.
Hence option (4) is correct option.
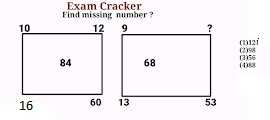
Problem # 8
1st Picture
(10)² - 16 = 100 - 16 = 84 in the same way
(12)² - 60 = 144 - 60 = 84
2nd Picture
(9)² - 13 = 81 - 13 = 68 in the same way
(?)² - 53 = 68
(?)² = 68 - 53
(?)² = 121
? = 11
so ? will take the value 11
Hence option (1) is correct option.
Also read these posts on Reasoning
1.Reasoning for competive exams
2 .Box and circle reasoning
3 . Reasoning for bank exams
4. Ten Tricky logical reasoning
5. Missing number series questions
6. Reasoning questions with answers
7. Circle Reasoning
8. Box Problems
9. 15 Questions Circle Problems
10. SSC CGL Reasoning
2 .Box and circle reasoning
3 . Reasoning for bank exams
4. Ten Tricky logical reasoning
5. Missing number series questions
6. Reasoning questions with answers
7. Circle Reasoning
8. Box Problems
9. 15 Questions Circle Problems
10. SSC CGL Reasoning
Problem # 9
Sum of all the numbers except middle number in 1st picture is equal to the middle number in 2nd picture.
5 + 2 + 7 + 5 = 19 (Middle number in 2nd picture).
Sum of all the numbers except middle number in 2nd picture is equal to the middle number in 3rd picture.
6 + 11 + 2 + 4 = 19 (Middle number in 3rd picture).
Sum of all the numbers except middle number in 2nd picture is equal to the middle number in 1st picture.
6 + 1 + 6 + ? = 15 (Middle number in 1st picture).
To make toal 15 in 1st picture ? will have to take 2 value in 3rd picture.
Hence option (4) is correct option.
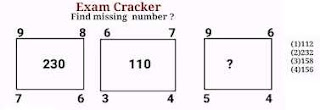
Problem # 10
Take the sum of squares of each number in the corner positions in each picture to get number the middle positions.
In 1st Picture
9² + 8² + 6² + 7² = 81 + 64 + 36 + 49 = 230
In 2nd Picture
6² + 7² + 4² + 3² = 36 + 49 + 16 + 9 = 110
In 3rd Picture
9² + 6² + 4² + 5² = 81 + 36 + 16 + 25 = 158
Therefore ? will take the value equal to 158
Hence option (3) is correct option.
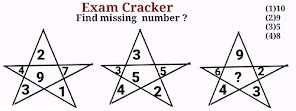
Problem # 11
Add all those numbers which are above central number then take the difference of this sum from the addition of those numbers which are below the central number .
1st figure ( 4 + 2 + 7 ) - ( 3 + 1 ) = 13 - 4 = 9 middle number
2nd figure ( 3 + 3 + 5 ) - ( 4 + 2 ) = 11 - 6 = 5 middle number
3rd figure ( 6 + 9 + 2 ) - ( 4 + 3 ) = 17 - 7 = 10 middle number
Hence option (1) is correct option.
Problem # 12
In this problem all the numbers written in 1st figure are related to 2nd figure and all the numbers written in 2nd figure are related to 3rd figure , similarly all the numbers written in 3rd figure are related to 4th figure .
i.e. number 4 in 1st figure is related to 10 in 2nd figure and number 10 in 2nd figure is related to 22 in 3rd figure. similarly number 22 in 3rd figure is related to 46 in 4th figure.
4 = 1st number in 1st figure
(4 × 2 ) + 2 = 10 ( 1st number in 2nd figure )
(10 × 2) + 2 = 22 ( 1st number in 3rd figure )
(22 × 2) + 2 = 46 ( 1st number in 4th figure )
1 = 2nd number in 1st figure
(1 × 2 ) + 2 = 4 ( 2nd number in 2nd figure )
(4 × 2) + 2 = 10 ( 2nd number in 3rd figure )
(10 × 2) + 2 = 22 ( 2nd number in 4th figure )
3 = Bottom number in 1st figure
(3 × 2) + 2 = 8 ( bottom number in 2nd figure )
(8 × 2) + 2 = 18 ( bottom number in 3rd figure )
(18 × 2) + 2 = 38 (The value of question mark)
Hence option (1) is correct option.Also Reads these posts on Reasoning
Reasoning Problems #11
Reasoning Analogy #10
Reasoning Questions #9
Circle Reasoning #8
Ten Box-Problems #7
Ten Reasoning problems #6
Ten-Important-Problem#5
Ten--Tricky-Puzzles #4
Twelve-Figures-Problems#3
Ten-Important-Reasoning#2
Picture-Reasoning#1

.jpg)