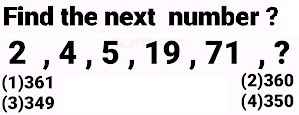Ten Number Analogy Reasoning Questions with Answers for Competitive Exams
Ten Most Important Number Analogy Reasoning questions with answers for competitive exams with solutions have been discussed in this post . These types of problems are very helpful for cracking competitive exams like ssc cgl, ssc chsl and various Bank exams and many other similar exams. please feel free to comment your opinions.
Number Analogy Reasoning questions with answers for competitive exams with solutions
Problem # 1
Problem # 2
Formula :-
2nd number = 1st number +1 = -4 +1 = -3





.jpg)








_11zon.jpg)
_11zon.jpg)