HOW TO FIND THE TRANSPOSE OF MATRIX WITH AN EASY METHOD
What is the Transpose of these Matrices ??
What is transpose of matrix, Method to find inverse of a matrix ,Matrices and Determinants in Most imp, How to find inverse of 3x3 Matrix, how to solve system of equation,matrix method of solving system of equations of three variables,determinant of 3x3 matrix calculator,
As it is clear from its name transpose means trans + pose i. e. transfer + position ( transfer of position ) , the transpose of any matrix is obtained by transfer of Rows into Columns And vice versa. i.e transforming 1st row to 1st column and transforming 2nd row to 2nd column and so on for 3rd ,4th and 5th rows and columns. This is very easy and interesting topic in matrices and determinants.How to find the Transpose of Matrix ,
As it is clear from its name transpose means trans + pose i. e. transfer + position ( transfer of position ) , the transpose of any matrix is obtained by transfer of Rows into Columns And vice versa. i.e transforming 1st row to 1st column and transforming 2nd row to 2nd column and so on for 3rd ,4th and 5th rows and columns. This is very easy and interesting topic in matrices and determinants.How to find the Transpose of Matrix ,
To find the transpose of the matrix
1st of all shift all the elements which are in 1st row to 1st column as
5
5
2
,then shift the elements which are in 2nd row to 2nd column as
-1
,then shift the elements which are in 2nd row to 2nd column as
-1
-3
7
similarly shift all the elements which are in 3rd row
to 3rd column as
4
2
8
And the matrix so obtained is the transpose matrix. We can check that same colour row have been transformed to same colour column
Now we shall take one example to find the transpose matrix
Here Given matrix have 3 rows and 4 columns .It means we shall have 4 rows and 3 columns in transpose matrix.
5
8
6
-4
8
6
-4
shift all the elements
which are in 2nd row to 2nd column as
3
5
8
3
5
8
3
shift all the elements
which are in 3rd row to 3rd column as
-3
8
-7
6
8
-7
6
so shifting the corresponding Rows into Corresponding columns. We can check that same colour rows are transformed to same colour columns.
Now we shall take one more example to find the transpose of matrix .Here Given matrix have 3 rows and 4 columns,It means we shall have 4 rows and 3 columns in transpose of that matrix.
7
-1
-2
5
shift all the elements which are in 2nd row to 2nd column as
4
4
3
3
shift all the elements which are in 3rd row to 3rd column as
8
6
-1
so shifting the corresponding Rows into Corresponding columns. We can that check same colour rows are transformed to same colour column.
Let us take an example Where A =
Step 1 Then on transforming 1st Column to 1st Row ,we have
4 -3 9 as 1st Row
Step 2 Then on transforming 2nd Column to 2nd Row ,we have
5 2 -2 as 2nd Row
||ly on transforming 3rd Column to 3rd Row ,we have
7 3 8 as 3rd Row
After taking Transpose A' will be
Let us take more example to find out the transpose of matrices. These are two examples , both of which are of 3×3 orders. Hence the transpose of these matrices will be again 3×3.

1st consider matrix G , after transforming its 1st row into column , the 1st column of the transpose matrix of G ' will be -2, -5, 4.
After transforming its 2nd row into column , the 2nd column of the transpose matrix of G ' will be -5, 7 , 3. And after transforming its 3rd row into column , the 3rd column of the transpose matrix of G ' will be 4, 3, 8. If we write the transpose of matrix G then we can see that there is no difference between the matrix G and the transpose of the matrix G.
Now consider matrix H , after transforming its 1st row into column , the 1st column of the transpose matrix of G ' will be 2, 3, 4.
After transforming its 2nd row into column , the 2nd column of the transpose matrix of H ' will be 3, 5 , 6. And after transforming its 3rd row into column , the 3rd column of the transpose matrix of H ' will be 4, 6, 7. Again in the case of matrix H , Matrix H and its Transpose matrix H ' are same.
Here is more interesting Example of Transpose of this Matrix,This matrix have 3 Rows and 3 columns,after taking Transpose this matrix still have 3 Rows and 3 columns,

1st consider matrix G , after transforming its 1st row into column , the 1st column of the transpose matrix of G ' will be -2, -5, 4.
After transforming its 2nd row into column , the 2nd column of the transpose matrix of G ' will be -5, 7 , 3. And after transforming its 3rd row into column , the 3rd column of the transpose matrix of G ' will be 4, 3, 8. If we write the transpose of matrix G then we can see that there is no difference between the matrix G and the transpose of the matrix G.
Now consider matrix H , after transforming its 1st row into column , the 1st column of the transpose matrix of G ' will be 2, 3, 4.
After transforming its 2nd row into column , the 2nd column of the transpose matrix of H ' will be 3, 5 , 6. And after transforming its 3rd row into column , the 3rd column of the transpose matrix of H ' will be 4, 6, 7. Again in the case of matrix H , Matrix H and its Transpose matrix H ' are same.
Now Take Transpose of this Matrix
what ?
Surprise to see that the Transpose of some of the Matrices are the Matrices Itself, i. e. if A¹= A
Such Matrices are called Symmetric Matrices.
Again if we take the transpose of the matrix given below and take -1 common from the matrix so obtained i .e this matrix will be equal to transpose of the negative of the transpose of the given matrix
then A¹ = - A , Such Matrices are called Skew Matrices.
Final words
This post was regarding what is transpose of matrix,finding the transpose of the matrix in matrices and determinants,Method to find inverse of a matrix ,Matrices and Determinants in Most imp, How to find inverse of 3x3 Matrix If you learn something from this post then share it with your friends and also follow me on my blog ,We shall meet again in next post , till then Good Bye ...........................
Final words
This post was regarding what is transpose of matrix,finding the transpose of the matrix in matrices and determinants,Method to find inverse of a matrix ,Matrices and Determinants in Most imp, How to find inverse of 3x3 Matrix If you learn something from this post then share it with your friends and also follow me on my blog ,We shall meet again in next post , till then Good Bye ...........................

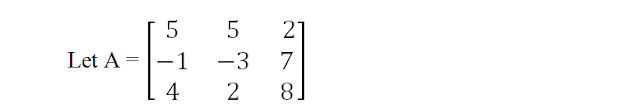
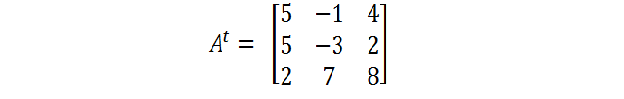















No comments:
Post a Comment
Your valuable suggestions are always acceptable to us for betterment of this website