Ten most important problems of Reasoning for competitive exam Part1

  No comments
Ten most important problems of Reasoning for competitive exam which includes missing numbers and missing terms and their solutions in reasoning analogy . These questions are very very important for upcoming competitive exams like SSC CGL ,SSC CHSL and RRB NTPC Etc

Ten most important problems of Reasoning for competitive exams

Reasoning for ssc cgl ,chsl, RRB NTPC

Solution 

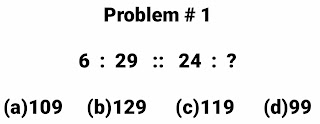
 6 is related to 29 in the same way 24 will be related to ? , It means we have to apply same mathematical operations to 24 to get ?.
So if we multiply 6 with 5  and then subtract 1 from result obtained in previous step like this ( 6 × 5 )  - 1 which will be equal to 29.
Same operation we have to apply  to 24.
( 24 × 5 ) - 1 = 120 - 1 =  119

So Correct  option is ( c ) 119

  Problem # 2


5  :  100   ::   7  :  ?
(a) 135   (b) 91   (c) 196  (d) 49


Solution

Because in 1st case if we take Square of  5 then multiply it with 4 we shall have 100.
5² × 4 = 25 × 4 = 100
Same procedure will be applied in 3rd number by taking square of 7 then multiply it with 4
7² × 4 = 49 × 4 = 196

Correct  option is  ( c  ) 196

Problem # 3

6  :  18   ::   4  :  ?
(a)4     (b)6     (c)8    (d)10


Solution 

Divide  6² by 2
6² ÷ 2 = 36 ÷ 2 = 18
Similarly divide 4² with 2
i.e.  4² ÷ 2 = 16 ÷2 = 8
Divide the square of 1st number by 2 to get 2nd number. Similarly take square of third number and then divide it by 2 to to get the number equal to? Since square of 4 is 16 then divided by 2 to get it.
6² ÷ 2 = 36 ÷ 2 = 18

4² ÷ 2 = 16 ÷ 2 = 8 

Correct  option is (  c ) 8


Problem # 4

18  :  30   ::   36  :  ?
(a)64   (b)  62   (c)54    (d) 66


Solution  

 (18 × 2 ) - 6  = 36 - 6 = 30
 (36 × 2 ) - 6  = 72 - 6 = 66
Multiply 1st number (18) with 2 and then subtract 6 from it
18 × 2 =  36 - 6 = 30
Similarly Multiply 3rd number ( 36 ) with 2 and then subtract 6 from it ,

36 × 2 = 72 - 6 = 66

correct  option is ( d) 66


Problem # 5

12  :  20   ::   30  :  ?
(a)48  (b)42    (c)15   (d)35


Solution 
Method 1  

Split 12  =  3 × 4 
Split  20  = 4 × 5, 
Split  30 =  5 × 6,  
Study these factors (3 , 4 ) , (4 ,5 ) ,(5 ,6 ) so next pair will be  ( 6 , 7 ) , It means ? Will be replaced by the number 6 × 7 = 42

Method 2 
12 will be written as square of 3 plus 3 , 20 will be written as square of 4 plus 4 ,30 will be written as square of 5 plus 5, so next number will be written as square of 6 plus 6 which is equal to 42 , Therefore   required option will be 42.
                         Or
Make continuous factors 3 and 4  , 4 and 5 ,5 and 6 and 6 and 7 of 12, 20, 30 and 42 respectively 
12 = 3 × 4  , 
20 = 4 × 5  ,
30 = 5 × 6 so 
42 = 6 × 7

Add same number to its square to get next number 
Or multiply next number to the number
 9  = 3² + 3   ,
 20 = 4² +4 ,
 30 = 5² + 5
42 = 6² + 6
Correct  option is ( b ) 42

  Problem # 6


12  :  54   ::   15  :  ?
(a)64   (b)69   (c)56  (d)67


Solution

{(1st number ) × 5} - 6 = 2nd number
(12 × 5) - 6 = 54
Multiply 3rd number with 5 then subtract 6 from it
{(3rd number ) × 5} - 6 = 4th  number
(15 × 5) - 6 = 69
Multiply first number ( 12 ) with 5 then subtract 6 from it to get 2nd number ( 54 ) ,   Similarly   Multiply third  number ( 15 ) with 5 then subtract 6 from it.
( 1 2 × 5  ) - 6 = 60 - 6 = 54
( 1 5 × 5  ) - 6 = 75 - 6 = 69
Correct  option is ( b) 69

Problem # 7

6  :  5   ::   8  :  ?
(a) 6      (b)10        (c) 2     (d)4 


Solution
Add 4 to 1st number and divide it with 2 to get 2nd number( 6 + 4 )/2 = 5
Similarly in 2nd case Add 4 to 3rd number then divide the resultant with 2 to get 4th number
( 8 + 4 )/2 = 6
Correct  option is ( a ) 6


Problem # 8

29  :  319  ::    23 :  ?

    (a)115  (b)252 (c)151  (d)46

Solution

Add both the digits of first number  i.e. 2 and 9 then multiply it with first number to get second number. similarly in the third number add both the digits I.e  2 and 3  and multiply it with 3rd number to get fourth number.
29 × ( 2 + 9 ) = 29 × 11 = 319
23 × ( 2 + 3 ) = 23 ×  5  = 115

So 253 is the right option (a) 115

Problem # 9

6  :  64   ::   11  :  ?

(a) 127      (b) 124     (c) 144    (d) 169


Solution

Add 2 to 1st given number and take its Square to get 2nd number. Similarly add 2 to 3rd number and take it square to get fourth number.
(6 + 2 )² = 8² = 64
(11 + 2)² = 13² = 169

Correct  option is ( d ) 169

Problem # 10

36  :  50   ::   64  :  ?
(a)70   (b) 82     (c)78      (d) 72


Solution

Take Square Root of 1st number and add 1 to it then add 1 to  its Square to get 2nd number.
Similarly take square root of 64 add 1 to its square  root and take it square and add 1  to get 4th number.
36 = 6² --->  (6 + 1)² + 1 = 50 ,

 64 = 8² ------> ( 8 + 1)² + 1 = 82
√36 = 6 add 1 to it = 7 , square this number = 49 + 1 = 50
√64 = 8 add 1 to it = 9 , square this number = 81 + 1 = 82

So  Correct option is ( b ) 82



Share:

Missing number in box Reasoning problem, How to solve various box problems

  12 comments

Reasoning of missing number in box problems will be discussed with the help of 10 most important examples. Some of these examples are of  3 × 3  order and other are of  3 × 4 orders . 

Reasoning of missing number in box problems

PROBLEM #  1


Reasoning of missing number in box problem

Step 1. 

Subtract the number in first column from the number in third column of every row. i. e. C3 - C1 = S

Step 2 . 

Multiply the the above difference with 3 to get the numbers in second column of every row i. e. C2 = 3S.

1st row    3 (48 - 28 ) = 3 × 20  = 60
2nd row 3 (7 - 5)  = 2 × 3 = 6
3rd row 3(27 - 14) = 3 × 13 = 39
4th row 3(16 - 7 ) = 3 × 9 = 27 
Hence required number is 27
Option (A) 27 is correct option

PROBLEM #  2


Reasoning of missing number in box problem

Every number in fourth row has been written as the square of all the numbers in 1st three rows in any particular column. 
Take the square of addition of  the elements of 1st three rows of 1st column like this
(1 + 4 + 2 )² = 7² = 49

Take the Take the square of addition of  the elements of 1st three rows of 1st column like this
(4 + 2 + 2 )² = 8² = 64

Take the square of addition of  the elements of 1st three rows of 1st column like this
 (? + 5 + 3 )² = (? + 8 )² = 169
(? + 8 )² = (13)² = 169 , Taking Square root
? + 8 = 13
? = 13 - 5 
? = 5
So required number will be 5
Option (C) 5 is correct option

PROBLEM #  3


Reasoning of missing number in box problem

Multiply all the numbers in the first three rows of every column and then divide the product by 2 to get the number in last row like this
(5×2×8)÷2 = 80÷2 = 40 ( Last number in 1st column ) 
(5×4×3)÷2 = 60÷2 = 30 ( Last number in 2nd column ) 
(2×1×10)÷2 = 20÷2 = 10 ( Last number in 3rd column ) 
So required number will be 10
Option (D)10 is correct option.


PROBLEM #  4


Reasoning of missing number in box problem

Adding both the numbers in second and third rows then multiply it with the number in First row to get the number in last row ,the process will be  repeated for all the three columns
( 6 + 7 ) × 5 = 65
( 3 + 2 ) × 4 = 20
( ? + 4 ) × 9 = 45
This implies ( ? + 4 ) = 45/9 = 5
? = 5 - 4 = 1
Hence required number is 1
Option (A) 1 is correct option.

PROBLEM #  5


Reasoning of missing number in box problem

Decrease the numbers in first  columns of every row by 1 then multiply it to get the number in third column of every row. 
1st Row  ( 8 - 1) ×  3  = 7 × 3 = 21
2nd Row  ( 6 - 1) ×  5 = 5 × 5 = 25
3rd Row  ( 12 - 1) ×  2 = 11 × 2 = 22
Hence required answer is 22
Option (B) 22  is correct option.

PROBLEM #  6


Reasoning of missing number in box problem

Add 1st two rows of each column to multiply with the number in 3rd column to get fourth number in every row. 
(5 + 4 ) × 2 = 9 × 2 = 18 (1st column 3rd row ) 
(6 + 3 ) × 3   = 9 × 3 = 27 ( 2nd column 3rd row ) 
(12 + 4 ) × ?  = 16 × ? = 96 (3rd column 3rd row ) 
16 × ? = 96
? = 6
Hence required number is 6
Option (D) 6  is correct option.


PROBLEM #  7




 First of all multiply  1st three numbers  in every Column then add the sum of 1st three  numbers in every row to  get the numbers in 4th row. i. e. formula for this problem is [ if a, b ,c and d are numbers in any column  then d = abc + (a+b+c) ]
[ ( 3 + 4 + 5) + (3 × 4 × 5 ) ] = 12 + 60 = 72
[ ( 2 + 5 + 6) + (2 × 5 × 6 ) ] = 13 + 60 = 73
[ ( 5 + 9 + 1) + (5 × 9 × 1 ) ] = 15 + 45 = 60
Hence  required number is 60
Option (D)60  is correct option.

Also study these missing number series questions


PROBLEM #  8



Reasoning of missing number in box problem

Decrease both the numbers in first and second columns of every row then multiply the reduced numbers to get the numbers in third column of every row
{ 8 - 1 }×{ 6 - 1 } = 7 × 5 = 35
{ 6 - 1 }×{ 4 - 1 } = 5 × 3 =  15 
{ 7 - 1 }×{ 5 - 1 } = 6 × 4 =  24
Hence required number is 24.
Option (A)24  is correct option.



PROBLEM #  9



Reasoning of missing number in box problem

Decrease the numbers in first column of every row and increase the numbers in second column of every row when multiplying both the reduced number of first and second column to get the numbers in third column of every row

{ 6 - 1 } × { 8 + 1 } = 5 × 9 = 45
{ 4 - 1 } × { 6 + 1 } = 3 × 7 = 21
{ 7 - 1 } × { 5 + 1 } = 6 × 6 = 36
Hence required number is 36
Option (C)36  is correct option.

PROBLEM #  10


Reasoning of missing number in box problem

Total of 1st row is  3 + 6 + 8 = 17
Total of 2nd row is  5 + 6 + 8 = 17
Total of 3rd row is  4 + 7 + ? = 17
Therefore replacing ? with 6 to get required answer.
Option (D)6  is correct option
So these were the most important box problems for many competitive exams

Do you like Missing number in box, Reasoning problem ?


Promoted content
 


Share:

Ten most important missing numbers questions and answers in reasoning

  No comments
Ten most important   missing numbers questions and answers in box problems in Reasoning Analogy in various figures of different order and types discussed in this post. These types of problems are very very important for the exams like SSC CGL ,SSC CHSL , RRB NTPC and many other similar competitive exams. 

Ten most important missing numbers questions and answers in reasoning


PROBLEM # 1

tricky puzzles with their Solutions

Since in 1st row we can write 3, 2 and 4  numbers to get 10 like this
( 3 × 2 ) + 4 = 6 + 4  = 10 (The number in last column  of 1st row )
And in 2nd row  ( 4 × 3 ) + 5 = 12 + 5 = 17, (The number in last column  of 2nd row )
In 3rd row ( 5 × 4 ) + 6 = 20 + 6 = 26 ,(The number in last column  of 3rd row )
Similarly ( 6 × 5 ) + 7 = 30 + 7 = 37 , (The number in last column  of 4th row )
So  " ? "   Will be replaced by 37 .
Therefore correct option will be (D)


PROBLEM # 2

   tricky puzzles with their Solutions              
Answer can be split into two parts, 1st part can be obtained by multiplying two given  numbers and second part can be obtained by adding these two numbers .
1st row 
5 × 3  = 15 and 5 + 3 = 8 so 5 , 3 = 158
2nd row 
9 × 1  = 9 and 9 + 1 = 10 so 9 , 1 = 910
3rd  row 
8 × 6  = 48 and  8 +6 = 14  so 8 , 6 = 4814
4th row 
4 × 4 = 16 and   4 + 4 = 8 so  4 , 4 = 168.
5th row
 7 × 3 = 21 and 7 + 3 = 10 so 7 , 3 = 2110
So ?  Will be replaced by 2110.
  Therefore correct option will be (A)



PROBLEM # 3


tricky puzzles with their Solutions

As the sum of 2nd and 3rd number in first and second rows in any particular column is equal to 1st element in that particular column so to get the value of " ? " . Take difference of first and second numbers column wise to get third number as follows.
44 +12 =  56, 
48 + 30 = 78 ,
14 + ? = 65 
➡️   ? = 65 - 14  = 51 
Therefore correct option will be (C)

PROBLEM # 4

tricky puzzles with their Solutions


Let us find relation between 3 and 18 , if we double the square of  3 ,we shall have 18. 
2 × (3²) = 2 × 9 = 18 (The number in last column  of 1st row )
And in 2nd row if we double the square of  4 ,we shall have 32
2 × (4²) = 2 × 16 = 32, (The number in last column  of 2nd row)
In the same way increasing the number one by one then  third ,fourth and  fifth columns can be calculated like this 

2 × (5²) = 2 × 25 = 50 (The number in last column  of 3rd row )
2 × (6²) = 2 × 36 = 72 (The number in last column  of 4th row )
2 × (7²)  = 2 × 49 = 98 (The number in last column  of 5th row )
Therefore correct option will be (C)

.

PROBLEM # 5


tricky puzzles with their Solutions

Formula a*b = (a × b) + (b - 1)

This the sum of two numbers , out of two ,1st number is product of two given  numbers and second  is the number one less than 2nd given number.

3 × 2 = (3 × 2) + (2 - 1) = 6 + 1 = 7
5 × 4 = (5 × 4) + (4 - 1) = 20 + 3 = 23
7 × 6 = (7 × 6) + (6 - 1) = 42 + 5 = 47
9 × 8 = (9 × 8) + (8 - 1) = 72 + 7 = 79
10 × 9 = (10 × 9) + (9 - 1) = 90 +8 = 98
Therefore correct option will be (C)

PROBLEM # 6



tricky puzzles with their Solutions

Suppose we have three numbers a , b and c then

Formula for this puzzle is = (a × b) + b or  b(a + 1)

Put a = 2 and  b = 6 in above formula ,we get

1st Line = (2  × 6)   +  6  = 12   +   6   = 18
Put a = 4 and  b = 20 in above formula to get 2nd line,we get
(4  × 20) + 20 = 80   +  20  = 100
Put a = 5 and  b = 21 in above formula to get 3rd line,we get
(6 × 21) + 21 = 126 +  21  = 147
So required and correct answer will be  6.


PROBLEM # 7

tricky puzzles with their Solutions

If in every row ,we add 1st and 3rd column and then multiply the sum with 2nd column, we shall have number in 4th column .

If we  consider three numbers a , b and c and start calculation by   
Formula =  (a × b) + (b × c)  or b(a + c)  --------(1)

To get 1st line , put a = 1 , b = 2 and c = 3 in (1) , we get 

1st Line =  (1×2) + (2×3) =2 + 6 = 8

To get 2nd line , put a = 2 , b = 3 and c = 4 in (1) , we get 

2nd  Line =  (2×3) + (3×4) = 6 + 12 =  18

To get 3rd line , put a = 3 , b = 4 and c = 5 in (1) , we get 

3rd Line =  (3×4) + (4×5) = 12 + 20  = 32

To get 4th line , put a = 4 , b = 5 and c = 6 in (1) , we get 

4th Line =  (4×5) + (5×6) = 20 + 30  = 50

Similarly Last line can be calculated by putting a = 5 , b = 6 and c = 7 in (1) , we get 

Last line  =  (5×6) + (6×7) = 30 + 42  = 72
Therefore correct option will be (D)

PROBLEM # 8 


tricky puzzles with their Solutions

Case 1

If we choose   1st number  as 5 then look at the pattern  opposite to given smaller number 
                              
5  ×  3 =  15
8  ×  3 =  24
12 × 3  =  36
In this pattern we can conclude 12 ×3 = 36

Case 2

If we choose   1st number  from ? then look at the opposite to given smaller number 
 ?    ×  3 = 12
5   ×  3  = 15
8   ×  3  = 24   
Therefore ? will be replaced  by 4.
Hence    4 ×  3  = 12


PROBLEM # 9


tricky puzzles with their Solutions

This circle can be divided into two parts ,  1st part containing the number 4 ,5 ,6 and 7 and second part containing 7 , 9 ,11 and ?.            Now study  the opposite number of 4  which is 7 . Then study the relation between other numbers and its opposite number ,we find difference between 4 and 7 is 3 , difference between 5 and 9 is 4 , difference between 6 and 11 is 5  . so in this pattern we can find difference between ' ? '  and  7 must be 6 . 
 7 - ? =  2 means ? = 5
  7 - 4 =  3
  9 - 5 =  4
 11 - 6 = 5 , the difference is increased by 1 every time .
  ?   - 7 = 6  means ? = 13
 Either 5 or 13 should be the required number, but 5 is not given in any option.
 So ? Will be replaced by 13 which is the required answer 
Therefore correct option will be (4)


PROBLEM # 10


tricky puzzles with their Solutions

We shall try every possible relation between different numbers given either row wise or column wise . It is found that there is no relation if we consider First row . 
 After elemination of 1st row we can develop a relation between 2nd ,3rd and 4th row which is multiplying the 2nd and 3rd numbers then double it to get 4th number column wise .
 2 × (7 × 4 ) = 2 × 28 = 56
2 × ( 15 × 6 ) = 2 × 90 = 180
2  × ( 8 ×  ?  ) = 80 
So ? = 5
These were the Ten most important  missing numbers questions and answers in reasoning . Please comment your opinion about this post. 

Therefore correct option will be (B) 

Share:

Ten most important problems of missing numbers in Reasoning Analogy part 2

  No comments

Series of missing numbers and missing terms and their  solutions in reasoning analogy . These questions are very very important for upcoming competitive exams like SSC CGL ,SSC CHSL and RRB NTPC Etc.


Ten most important problems of missing numbers in Reasoning Analogy


Problem # 1

problems of missing numbers in Reasoning Analogy

This series consists of two alternate series. 1st series consist of number 1, 3, 5 and 7 and second series consist of  the series 2 , 5 , 8 , ?
So in 1st series there is difference of 2, so next number in the series must be 2 greater than 7 i.e. 9 
In the 2nd series  we observed a difference of 3 show the next number must be 11 that is 3 greater than 8 the last term therefore the last two terms of the series 11 and 9.

The correct option is  (1) 11,9

Problem # 2

problems of missing numbers in Reasoning Analogy

This series is also the combination of two series one with the number  2, 48 ,16 ,32 and second series consist of these numbers 6, 9 13 ,18 , ? . So ? Will be filled out using 2nd series not from 1st series.

Observing 2nd series carefully ,In  second series numbers are increased by  3 ,4 and 5 ,so next Increment should be of 6. This implies next number should be  24 with an increment of 6.

The correct option is  (1)24 

Problem # 3

problems of missing numbers in Reasoning Analogy

Observe carefully all the numbers in the series are prime number , so  next prime number after 37 will be 41 .This implies that  ?  will be replaced by 41.

The correct option is  (3)41 

Problem # 4

problems of missing numbers in Reasoning Analogy

All the numbers in this series are consisting of three digits numbers and Middle digit is the sum of first and last digit in all the numbers except one that is 342 in this case 3 + 2 is equal to 5 not equal to 4 .So  correct option is option is  (c) ,this is the wrong number in the series .

The correct option is  (3)342 

Problem # 5

problems of missing numbers in Reasoning Analogy

Every number in this series is the sum of its two  preceding number plus 3.

14  = ( 7 + 4 ) + 3
24 = ( 14 + 7 ) + 3
41 = ( 24  +14 ) + 3
?   = ( 41 + 24 ) + 3 = 65+3 = 68

The correct option is  (3)68 

Problem # 6


problems of missing numbers in Reasoning Analogy

This series consists of triplet ,that is every third number is product  its two preceding numbers

  As third  number 10 is the product of 2 and 5, sixth number  18 is the product of fourth (3) and fifth (6 ) numbers .

So ninth number of the series  must be the product of seventh and  eighth numbers. 4 × 7 = 28 instead of 30

The correct option is  (3) 30

Problem # 7


problems of missing numbers in Reasoning Analogy

Here second  number is the sum of the digits of first number the forth number is the sum of digits of third number similarly every even positioned number is  the sum of its preceding number's digits question  mark will be replaced by the sum of 5 + 3 that is 8

The correct option is  (1)8 

Problem # 8

problems of missing numbers in Reasoning Analogy

Writing 3 = 2² - 1

Writing 8 = 3² - 1

Writing  15 = 4² - 1

Writing 24 = 5² - 1


Show next number should be  6² - 1 (6  square minus 1 ) that is 35

Writing  6² - 1 = 35

The correct option is  (2)35 

Problem # 9

problems of missing numbers in Reasoning Analogy

Every number in this series is the double of its preceding number .So double of 1 is   2 , double of 2 is 4 ,double of 4 should be 8 ( instead of 7 ) , double of 8 is 16 and double of 16 should be 32 .  So 7 is the wrong number in this series.

The correct option is  (1)7 

Problem # 10


problems of missing numbers in Reasoning Analogy

In the series every number is the the cube of its  position plus 1 .

Since

  2 =  1³ + 1

   9 =  2³ + 1

  28 =  3³ + 1

  65  =  4³ + 1

  126 =  5³ + 1

 In the same way next number of the series must be  6³ + 1 = 216 + 1 = 217

The correct option is  (1) 217

How-to-Solve-hard-and-impossible-Puzzles


TO CRACK  ANY COMPETITIVE EXAM VISIT THIS YOUTUBE CHANNEL FOR MATHS AND REASONING 

EXAM CRACKER

My previous Post


FINAL WORDS

  Thanks for watching and responding to this post of reasoning based on mathematics and number sequence puzzle solver.

Appeal 


If you are a mathematician Don't forget to visit my Mathematics You tube channel ,Mathematics Website and Mathematics Facebook Page , whose links are given below



Also watch this video 



Share: