Memorise A B AND C D Formulas In Trigonometry in an Easy Manner
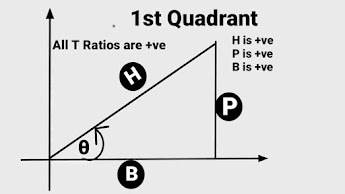
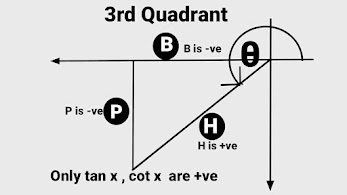
Welcome to this post of learning trigonometric formulas .Most of the Students or Mathematics Learner ,most of the time confuse to remember or memorise A B and C D formulas, They mixed A B and C D formulas with each other and could not reproduce what they have learnt . So today we going to learn new techniques to learn "How to memorise AB and CD formulas" forever. Before this we must have knowledge of different trigonometric values of different angles in different quadrants.
Start with sine of angle A and multiply it with cosine of angle B and in other part i. e. After +ve sign Start with Cosine of angle A and multiply with Sine of angle B. i.e start with sine and ends with sine and in middle both the terms are cosine ,and angles start with A then B again A then again B.
Start with cosine of angle A and multiply it with cosine of angle B and in other part i. e. After +ve sign Start with Sine of angle A and multiply with Sine of angle B. i. 1st and 2nd terms are cosine and 3rd and 4th terms are sine , and angles start with A then B again A then again B.
Want to Learn What is Set , Types of Sets , Union, Intersection of Sets And Venn Diagrams
Want to learn Matrix , Different Types of matrices And Determinants.
Want to learn How to Solve Linear Equations of Two and Three Variables || Matrix Method to Solve System of Linear Equations.
First of all have a quick look at some of these formulas
AB Formulas
| S N | Fomula | Result |
|---|---|---|
| 1 | sin (A + B) | sin A cos B + cos A sin B |
| 2 | sin (A - B) | sin A cos B - cos A sin B |
| 3 | cos (A + B) | cos A cos B - sin A sin B |
| 4 | cos (A - B) | cos A cos B + sin A sin B |
To clear all your doubts on " How to Calculate Different Trigonometric values in different quadrants " in an easy Method. Click on the above links .
Tricks to Learn A B Formulae For sine angles
When angles are added i. e Sin ( A+B )
When Angles are added and then their Trigonometric Ratios is
taken , and if we have to take the Sine
of added angles, then it can be done
like this.
Start with sine of angle A and multiply it with cosine
of angle B and in other part i. e. After
+ve sign Start with Cosine of angle A and multiply with
Sine of angle B. i.e. start with sine and ends with sine and in middle both the
terms are cosine ,and angles start A
then B again A then again B.
Sin (A+B) = Sin A Cos B + Cos A Sin B
When angles are subtracted i. e
Sin ( A-B )
When Angles are subtracted and their Trigonometric Ratios is taken , and
if we have to take the Sine of subtracted angles, then it can be done like this
Start with sine of angle A and multiply it with cosine of angle B and in other part i. e. After +ve sign Start with Cosine of angle A and multiply with Sine of angle B. i.e start with sine and ends with sine and in middle both the terms are cosine ,and angles start with A then B again A then again B.
Sin (A - B) = Sin A Cos B - Cos A Sin B
Tricks to Learn A B Formulae For Cosine angles
When angles are added i. e
Cos ( A+B )
When Angles are added and then their
Trigonometric Ratios is taken , and if we have to take the Cosine of
added angles, then it can be done like this.
Start with cosine of angle A and multiply it with cosine of angle B and in other part i. e. After -ve
sign Start with Sine of angle A and
multiply with Sine of angle B. i.e. 1st and 2nd terms are cosine and
3rd and 4th terms are sine , Angles start with A then B again A then again B.
"Here Sum of cosine of Two angles
is equal to difference of product
of cosines of both the angles and product of sine of both the angles ".
Cos (A+B) = Cos A Cos B - Sin A Sin B
When angles are subtracted i. e
Cos ( A-B )
When Angles are subtracted
and then their Trigonometric Ratios is
taken , and if we have to take the cosine
of subtracted angles, then it can be done like this.
Cos (A - B) = Cos A Cos B + Sin A Sin B
Start with cosine of angle A and multiply it with cosine of angle B and in other part i. e. After +ve sign Start with Sine of angle A and multiply with Sine of angle B. i. 1st and 2nd terms are cosine and 3rd and 4th terms are sine , and angles start with A then B again A then again B.
"Here Difference of cosine of
Two angles is equal to the Sum of
product of cosines of both the
angles and product of sine of both the
angles" .
Want to Learn What is Set , Types of Sets , Union, Intersection of Sets And Venn Diagrams
How to Memorise C D Formulae
To learn C D formulae
Step 1
Place 2 for all four formulae and take Trigonometric Ratio of 1st angle for all four formulae which is (C+D)/2 and again trigonometric Ratio of 2nd angle which is (C-D)/2.
Step 2.1
For addition of Sine Formula start with sine of 1st angle as mentioned in step 1 and multiply it with cos of 2nd angle as mentioned in step 1.
Step 2.2
For subtraction of Sine Formula start with cosine of 1st angle as mentioned in step 1 and multiply it with sine of 2nd angle as mentioned in step 1.
Step 3.1
For addition of cosine Formula start with cosine of 1st angle as mentioned in step 1 and multiply it with cosine of 2nd angle as mentioned in step 1.
Step 3.2
For subtraction of cosine Formula start with sine of 1st angle as mentioned in step 1 and multiply it with sine of 2nd angle as mentioned in step 1,and do not forget to multiply it with -ve sign.
or
If you do not want to multiply it with -ve sign ,then you can change 2nd angle (D-C)/2 instead of (C-D)/2
CD Formulas
| S N | Fomula | Result |
|---|---|---|
| 1 | sin C + sin D | 2 sin {(C+D)/2} cos {(C-D)/2} |
| 2 | sin C - sin D | 2 cos {(C+D)/2} sin {(C-D)/2} |
| 3 | cos C + cos D | 2 cos {(C+D)/2} cos {(C-D)/2} |
| 4 | cos C - cos D | -2 sin {(C+D)/2} sin {(C-D)/2} |
| or | cos C - cos D | 2 sin {(C+D)/2} sin {(D-C)/2} |
Want to learn How to Solve Linear Equations of Two and Three Variables || Matrix Method to Solve System of Linear Equations.
A quiz of mathematics for you
Conclusion
Thanks for devoting your valuable time for the post Easy Tricks to Memorise A B and C D Formulae in Trigonometry and Trigonometry 's shortcut formulas of this blog ,trigonometry formulas for class 11 ncert,trigonometric functions class 11 notes, trigonometry class 11 tricks,,trigonometry formulas list,. If you found this this blog/post of your concern, Do Follow me on my blog and share this post with your friends . We shall meet again in next post ,till then Good Bye.
How to Memorise A B and C D formulas easily ,watch this video