Ten Questions of missing numbers for competitive exams and missing number in reasoning for competitive exams like Bank PO, Bank clerk, SSC CGL, ssc chsl, RRB NTPC , group D etc have been discussed in this post .
Ten Questions of number analogy for competitive exams
Problem # 1
Formula :- (Sum of both digits of 1st number) × ( Sum of both digits of 2nd numbers) .
(3 + 5 ) × (6 + 5) = 8 × 11 = 88 ( It is given)
(3 + 6 ) × (7 + 4) = 9 × 11 = 99 ( It is given)
(4 + 4 ) × (5 + 5) = 8 × 10 = 80 ( The value of question mark )
Option (4) 80 is correct option
Problem # 2
To find the value of question mark, 1st multiply both the digits of 1st number and add both the digits of 2nd number and then multiply the results so obtained.
Formula :- (Product of both digits of 1st number) × (Sum of both digits of 2nd number).
(2 × 7) × ( 3 + 4 ) = 14 × 7 = 98
(1 × 6 ) × ( 3 + 4 ) = 6 × 7 = 42
(2 × 8 ) × ( 3 + 3 ) = 16 × 6 = 96
Option (3)96 is correct option
Problem # 3
In this problem all the three given numbers are nearer to the cube of any number. Hence all the given numbers can be written as the cube of some number in addition to one more mathematical operation. If we look carefully then all these given numbers can be written as the sum of a number and cube of the same number.
Formula :- a³ + a
8³ + 8 = 512 + 8 = 520 (1st number in given problem)
9³ + 9 = 729 + 9 = 738 (2nd number in given problem)
6³ + 6 = 216 + 6 = 222 (3rd number in given problem)
7³ + 7 = 343 + 7 = 350 (4th number in given problem) and this will be the value of question mark.
Option (4)350 is correct option
Problem # 4
In this reasoning problem 1st number (167) is associated to 43 with the help of any rule , in the same rule we have to associate 245 to a number out of four given option.
Look carefully the given numbers consists of three digits. These three digits can be utilised with the help a formula given below.
Formula :- (Left most digit) +{middle digit × right most digit}
{ 1 + ( 6 × 7) } = 1 + 42 = 43
{ 2 + ( 4 × 5) } = 2 + 20 = 22
Option (1)22 is correct option
Problem # 5
In this reasoning problem 1st number (167) is associated to 112 with the help of some rule , With the help of same rule we have to associate 452 to a number out of four given option. Also in this problem all the numbers consists of three digits. These three digits can be used to find the value of question mark with the help a formula given below.
Formula :- (Two Left most digits × right most digit}.
In this problem both the left most digits can be taken as single unit to multiply with the 3rd number.
{ 16 × 7 } = 112
{ 45 × 2 } = 90 = ? ( The value of question mark )
Problem # 6
In this reasoning problem 1st number (824) is associated to 3 with the help of any rule , in the same way we have to associate 999 to a number out of four given option. All the three digits of given numbers can be utilised with the help a formula given below.
Formula :- (Two Right most digits ÷ Left most digit}
In this problem both the two right most digits can be taken as single unit to get divided with the 3rd number.
24 ÷ 8 = 3
99 ÷ 9 = 11= ? ( The value of question mark)
Option (2)11 is correct optionProblem # 7
This reasoning problem also consists of three digits .In this problem we have to transform 124 to 21 using a rule in the same way we have to change 631 to a number out four given options. To solve this problem means to get the 2nd number from 1st number ,take the squares of all the digits of 1st number and add all the three results so obtained.
Formula :- (1st digit)² + (2nd digit)² + (3rd digit)²
1² + 2² + 4² = 1 + 4 + 16 = 21
6² + 3² + 1² = 36 + 9 + 1 = 46 =? ( The value of question mark)
Option (3)46 is correct option
Problem # 8
This reasoning problem also consists of three digits . In this problem we have to transform 124 to 69 using any rule in the same way we have to change 521 to a number out four given options. To solve this problem means to find the value of 2nd number in this figure , calculate the sum of 1st digit , squares of middle digit and cube of 3rd digit .
Formula :- (1st digit) + (2nd digit)² + (3rd digit)³
1 + 2² + 4³ = 1 + 4 + 64 = 69
5 + 2² + 1³ = 5 + 4 + 1 = 10= ? ( The value of question mark)
Option (4)10 is correct option
Also Reads these articles
Start
End
Problem # 9
In this reasoning problem 1st number (424) is associated to 96 with the help of any rule , in the same rule we have to associate 521 to a number out of four given option. These three digits can be utilised with the help a formula given below.
Formula :- (Two Right most digits × Left most digit}
In this problem both the right most digits can be taken as single unit to multiply with the 1st number.
4 × 24 = 96
5 × 21 = 105 = ? ( The value of question mark)
Option (1)105 is correct option
Problem # 10
Formula :- (1st digit) + (2nd digit) + (3rd digit)
5 + 3 + 8 = 16
7 + 2 + 5 = 14 Sum of digits is 2 lees than above sum
8 + 1 + 3 = 12
We have to choose that option whose sum of digits must be 2 less than above sum. Therefore
7 + 1 + 2 = 10
Since all the three remaining option have total other than 10.
8 + 1 + 4 = 13
2 + 1 + 9 = 12
3 + 2 + 8 = 13 = ? ( The value of question mark)
Option (2)712 is correct option
7 + 2 + 5 = 14 Sum of digits is 2 lees than above sum
8 + 1 + 3 = 12
We have to choose that option whose sum of digits must be 2 less than above sum. Therefore
7 + 1 + 2 = 10
Since all the three remaining option have total other than 10.
8 + 1 + 4 = 13
2 + 1 + 9 = 12
3 + 2 + 8 = 13 = ? ( The value of question mark)
Option (2)712 is correct option
Conclusion
Comment your valuable suggestion regarding the post most important Reasoning questions with answers which includes reasoning for competitive exams, circle problems, box problems, circle problems and triangles problems for competitive exams like SSC CGL ,SSC CHSL ,CPO ,Bank exams and RRB NTPC etc which were explained in this post.


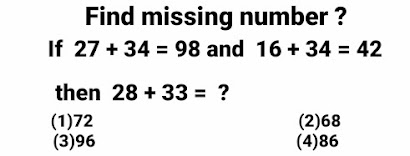








No comments:
Post a Comment
Your valuable suggestions are always acceptable to us for betterment of this website