USING METHOD OF INTEGRATION ,HOW TO FIND AREA OF TRIANGLE BOUNDED BY THREE LINES
Using method of integration find the area of triangle,using the method of integration find the area of the region bounded by the lines,area of triangle by integration method
Using Method of Integration , How to find the area of triangle bounded by three lines
2x + y = 0 , 3x - 2y = 6 and x - 3y + 5 = 0Solution
Given lines are
3x - 2y = 6 --------- (2) and
x - 3y = -5 --------- (3)
If these lines are intersecting then we have to find their coordinates of points of intersection .
To Find Coordinate of Point A
Multiply (1) by 2 and adding to (2) , we get4x + 2y + 3x - 2y = 8 + 6
7x = 14 ⇒ x =2
Putting x = 2 in (1) , we get
 |
| Area under Curve |
4 + y = 4 ⇒ y = 0
∴ (1) and (2) meets at point A(2,0).
To Find Coordinate of Point B
To find point of intersection (2) and (3);Multiply (3) by -3 and adding to (2) , we get
3x - 2y -3x +9y = 6 +15
7y = 21 ⇒ y = 3
Putting y = 3 in (3) , we get
x-3(3) = -5
⇒ x = -5 +9 ⇒ x = 4
∴ (2) and (3) meets at point B(4,3).
To Find Coordinate of Point C
To find point of intersection (1) and (3);Multiply (1) by 3 and adding to (3) , we get
6x + 3y + x - 3y = 12 - 5
7x = 7 ⇒ x =1
Putting x = 1 in (1) , we get
2(1) + y = 4
⇒ y =4 - 2 ⇒ y = 2
∴ (1) and (3) meets at point C(1,2).
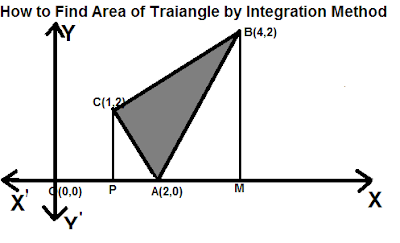
we get points of intersection of (1) and (2) A(2,0), points of intersection of (2) and (3) B(4,3) and points of intersection of (1) and (3) C(1,2).
Required Area = Shaded Area = Area DCBED - Area DCAD -Area ABEA
For better understanding watch this video
Conclusion
If you are a mathematician Don't forget to visit my Mathematics You tube channel ,Mathematics Website and Mathematics Facebook Page , whose links are given below









Thanks for sharing this article here about the calculation of the Perimeter Of A Triangle. Your article is very informative and I will share it with my other friends as the information is really very useful. Keep sharing your excellent work.
ReplyDelete