WHAT ARE LINEAR INEQUALITIES AND HOW TO SOLVE INEQUALITIES GRAPHICALLY
Today we are going to discuss linear inequalities , solving inequalities , linear inequations of one variable , linear inequalities in two variables , graphing inequalities , solving linear inequalities , system of linear inequalities , linear inequalities examples , application of linear inequations and its formation with the help of some examples.
Linear Inequation
An Inequation is a statement which involve the sign of Inequality < , > , ≤ , ≥ , ≠ etc
An equation which contains variables of 1st degree and does not contains product of variables is called Linear Inequation .
3x + 5 < 2 , 6x - 5 > 7 , 1 - 3x > 10 , 2x - 3 ≤ 5
These are called Linear Inquations Of One Variable.
3x - 5y ≤ 15 , 4x+3y ≥ 12 ,
6x - 4y < 24 , 3x + 5y ≥ 15,
2x - 5y ≤ 10, 3x + 7y ≥ 21,
These are called Linear Equations Of two Variables .
Solve the Inequation 1 - 2x < - 8
1 - 2x < - 8
Shifting the constant term to R.H.S.
⇒ - 2x < - 8-1
⇒ - 2x < - 9
Isolating x from L.H.S by dividing with -2 on both sides and change the sign of Inequality.
Note : Whenever we divide or Multiply any Inequality with minus number ,then the sign of that inequality changes , i.e. < to > and < to > or ≤ to ≥ and ≤ to ≥ .
⇒ - 2x/-2 > - 9/-2
⇒ x > 9/2
It means every values greater than 9/2 will satisfy the given Inequality
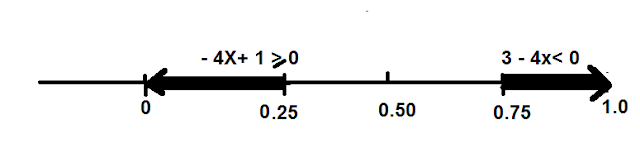
Solve the Inequalities -4x + 1 ≥ 0 , 3 - 4x < 0
Consider 1st Inequality
- 4x + 1 ≥ 0 Shifting 1 to RHS
⇒ - 4x ≥ 0 -1 Dividing with -4 on both sides to isolate x
⇒ - 4x /-4 ≥ - 1/ -4 ,change the sign of Inequality
⇒ x ≤ 1/4 = 0.25 -------(1)
Consider 2nd Inequality
⇒ 3 - 4x < 0 Shifting 3 to RHS
⇒ - 4x < -3 Dividing with -4 on both sides to isolate x
⇒ -4x/-4 < -3/-4 , change the sign of Inequality
Solve -12 ≤ 4 -3x -5 < 2
Given - 12 ≤ 4 -3x -5 < 2 ,
To solve such types of Inequality Multiply throughout by -5 ( i. e. with denominator ) , if the multiplicand is negative then change the sign of all the inequalities
⇒ -12×(-5) ≥ 4 -3x -5 × (-5) > 2 × (-5) ,
⇒ 60 ≥ 4 - 3x > -10 ,
Add or Subtract the -ve of constant number appearing with x (Here -ve of 4 ) to eliminate the constant term in middle of the inequality .
⇒ 56 ≥ - 3x > -14 ,
Divide with co-eff of x to isolate "x" i. e with -3
⇒ 56/-3 ≤ - 3x/-3 < -14/-3
⇒ 56/-3 ≤ - 3x/-3 < -14/-3
⇒ All those values which are between -563 and 143 are solution of given Inequality .
This video will help in understanding Linear Inequalities
Solve 2x -3 4 + 8 ≥ 2+ 4x 3 and represent the Solution in number line
Given
2x - 3 4 + 8 ≥ 2 + 4x 3
To find the solution of such inequality where different denominators have two different number , we just multiply with the product of these two numbers which are in the denominators (Here 4 × 3 = 12 ) to each term of the inequality
⇒ 2x - 3 4 × 12 + 8 ×12 ≥ 2 × 12 + 4x 3 × 12
⇒ (2x - 3) × 3 + 96 ≥ 24 + ( 4x ) × 4
⇒ 6x - 9 + 96 ≥ 24 + 16x
⇒ 6x + 87 ≥ 24 + 16x
⇒ 6x - 16x ≥ 24 - 87
⇒ - 10x ≥ - 63 , Change the inequality sign after multiplication / division with -ve number
Solve - 3 ≤ 4-7x2 ≤ 18
Given - 3 ≤ 4-7x2 ≤ 18 ,
To Eliminate 2 from denominator Multiply every term with 2
To Eliminate 2 from denominator Multiply every term with 2
⇒ - 3 × 2 ≤ 4-7x2 × 2 ≤ 18 × 2
⇒ -6 ≤ 4 -7x ≤ 36
⇒ -6 - 4 ≤ - 4 + 4 -7x ≤ - 4+ 36
⇒ -10 ≤ -7x ≤ 32
⇒ -10/-7 ≥ -7x/-7 ≥ 32/-7 , change the sign of inequality
⇒ 10/7 ≥ x ≥ -32/7
⇒ 10/7 ≥ x ≥ -32/7
Hence set of all those numbers lying between 10/7 and -32/7 is the solution of the given inequality
Draw the Diagram of the solution set of the constraints : x ≥ 0 ; y ≥ 0 , 4x + 7y ≤ 28
In order to solve such a constraints , 1st of all draw graph of linear Equations x = 0 (which is known as y axis) , y = 0 ( which is known as x-axis ) , 4x + 7y = 28 simultaneously .
As we know that graph of the line x = 0 is the line y - axis and graph of the line y = 0 is the line x - axis .
Now to draw the graph of line 4x + 7y = 28 , Put x = 0 and y = 0 in given line respectively and find the values of y and x . So if x = 0 in the equation , we get y = 4 , and when we put y = 0 in line 4x + 7y = 28 , we get x = 7 .
Therefore If x = 0 then y = 4
and If x = 7 then y = 0
we get two points A(0,4) and B(7,0) .
Now check the feasible region of each lines , as x ≥ 0 implies right half of the Cartesian plan ( including y - axis ) and y ≥ 0 implies upper half of the Cartesian plan ( including x - axis ) . So from these two inequalities we get the 1st quadrant as the common/feasible region .
Now plots both the points A(0,4) and B(7,0) in the plan and draw a line passing through these two points.
Now put (0,0) point in the inequality 4x + 7y ≤ 28 , If it comes out true then feasible region will be toward origin and if it comes out false then feasible region will be away from origin .
Now mark the common region from all the inequalities and shade it , The shaded region will be the required/feasible region after graphing linear inequalities or system of inequalities . i.e The solution of the given constraint.
As we know that graph of the line x = 0 is the line y - axis and graph of the line y = 0 is the line x - axis .
Now to draw the graph of line 4x + 7y = 28 , Put x = 0 and y = 0 in given line respectively and find the values of y and x . So if x = 0 in the equation , we get y = 4 , and when we put y = 0 in line 4x + 7y = 28 , we get x = 7 .
Therefore If x = 0 then y = 4
and If x = 7 then y = 0
we get two points A(0,4) and B(7,0) .
Now check the feasible region of each lines , as x ≥ 0 implies right half of the Cartesian plan ( including y - axis ) and y ≥ 0 implies upper half of the Cartesian plan ( including x - axis ) . So from these two inequalities we get the 1st quadrant as the common/feasible region .
Now plots both the points A(0,4) and B(7,0) in the plan and draw a line passing through these two points.
Now put (0,0) point in the inequality 4x + 7y ≤ 28 , If it comes out true then feasible region will be toward origin and if it comes out false then feasible region will be away from origin .
Now mark the common region from all the inequalities and shade it , The shaded region will be the required/feasible region after graphing linear inequalities or system of inequalities . i.e The solution of the given constraint.
Also Read HOW TO SOLVE HARD AND IMPOSSIBLE PUZZLES PART 3
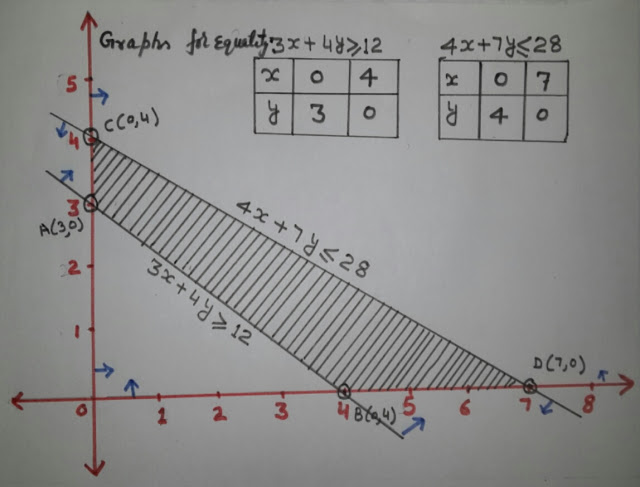
Solve Graphically the System of Linear constraint : 3x + 4y ≥ 12 ; 4x + 7y ≤ 28 ; x ≥ 0 ; y ≥ 0
As we know from previous problem x ≥ 0 ; y ≥ 0 the common region from these two inequalities is in 1st quadrant.
Now Draw the graphs for two lines 3x + 4y = 12 and 4x + 7y = 28 .
Now Draw the graphs for two lines 3x + 4y = 12 and 4x + 7y = 28 .
Put x = 0 and y = 0 in 1st equation , we get y = 3 and x = 4 respectively . Therefore two points will be A(0,3) and B(4,0) .
Similarly put x = 0 and y = 0 in 2nd equation respectively , we get y = 4 and x = 7 respectively .Therefore two points will be C(0,4) and D(7,0) .
Now plots both the points A(0,3) and B(4,0) in the plan and draw a line passing through these two points. Also plots both the points C(0,4) and D(7,0) in the plan and draw a line passing through these two points.
Now put (0,0) point in the inequality 3x + 4y ≥ 12 and 4x + 7y ≤ 28 , If it comes out true then feasible region of that inequality will be toward origin and if it comes out false then feasible region of that inequality will be away from origin .
Solve Graphically the System of Linear constraint 2x+3y ≥ 6 ; x - 2y ≤ 2 ; 6x + 4y ≤ 24 ; -3x +2y ≤ 3 x≥ 0 ; y ≥ 0
As from previous problems x ≥ 0 ; y ≥ 0 the common region from these two inequalities is in 1st quadrant.
Now Draw the graphs for two linear lines 2x + 3y = 6 ; 6x + 4y = 24 and -3x +2y = 3 .
Now Draw the graphs for two linear lines 2x + 3y = 6 ; 6x + 4y = 24 and -3x +2y = 3 .
Put x = 0 and y = 0 in 1st equation 2x + 3y = 6 , we get y = 2 and x = 3 respectively . Therefore two points will be A(0,2) and B(3,0) .
Now put x = 0 and y = 0 in 2nd equation x - 2y = 2, we get y = -1 and x = 2 respectively .Therefore two points will be C(0,-1) and D(2,0) .
Put x = 0 and y = 0 in 3rd equation 6x + 4y = 24 , we get y = 6 and x = 4 respectively . Therefore two points will be E(0,6) and F(4,0) .
Also Put x = 0 and y = 0 in 1st equation -3x + 2y = 3, we get y = 3/2 and x = -1 respectively . Therefore two points will be G(0,3/2) and H(-1,0) .
Now plots both the points A(0,2) and B(3,0) in the plan and draw a line passing through these two points. Also plots both the points C(0,-1) and D(2,0) in the plan and draw a line passing through these two points.
Also plots both the points E(0,6) ,F(4,0) and G(0,3/2) and H(-1,0)
in the plan and draw a line passing through these two points. therefore there will be four lines in 1st quadrant.
Now put (0,0) point in the inequality 2x + 3y ≥ 6 ; x - 2y ≤ 2 ; 6x + 4y ≤ 24 ; -3x + 2y ≤ 3 , If it comes out true then feasible region of that inequality will be toward origin and if it comes out false then feasible region of that inequality will be away from origin .
At last mark common region from all the inequalities x ≥ 0 ; y ≥ 0 ; 3x + 4y ≥ 12 and 4x + 7y ≤ 28 and shade it , The shaded region will be the required/feasible region. ( As shown in the figure above ) i.e. This is the solution of the given constraint.
Also Read : Sets , Types of Set , Union ,Intersection , Complement of set and venn Diagrams
Application of Linear Inequalities
Problem : In the first four papers each of 100 marks , Ravi got 99 , 88 , 77 , 96 marks . If he wants an average of ≥ 80 marks and ≤ 85 marks , Find Find the range of Marks he should score in the fifth paper .
Let Marks secured by Ravi in Fifth Paper = x
Then as we know that average is the sum of the marks secured in
five papers and divided by 5. Then according to given conditions the average must be grater than 80 and less than 85. Then Mathematically it can be translated in linear equation as follows
80 ≤ 99+88+77+96 + x 5 ≤ 85
80 ≤ 360 + x 5 ≤ 85 ,
Now Multiplying with 5 to eliminate denominator
80 × 5 ≤ 360 + x 5 × 5 ≤ 85 × 5 ,
400 ≤ 360 + x ≤ 425 ,
Subtracting 360 throughout the inequation
40 ≤ x ≤ 65
- It means in order to get average of greater than equal to 75 and less than equal to 85 marks , he should score in the range of 40 to 65 marks in the Fifth Paper.
Problem : The longest side of a triangle is twice the shortest side and the third side is 2 cm longer than the shortest side . If the perimeter of the triangle is more than 166 cm then find the minimum length of the shortest side.
It is given that longest side is twice the shortest side
∴ Longest side of triangle = 2x cm,
given that third side is 2 cm longer than shortest side.
∴ Third side of triangle = x + 2 cm
Then translating these line to mathematical form ( perimeter of triangle is more than 166 ) , we get
( x ) + ( 2x ) + ( x + 2) > 166
⇒ 4x + 2 > 166
⇒ 4x > 166 - 2
⇒ 4x > 164
⇒ x > 166 /4
⇒ x > 41
This implies the shortest side of the triangle must be 41 cm in order to satisfies all the conditions .
Perimeter : Perimeter of a triangle is the sum of all the sides of given triangle .
Conclusion
In this post I have discussed Linear Inequations , linear inequations of one variable , solving linear inequalities, graphing linear inequalities,system of inequalities, linear inequalities in two variables, system of linear inequalities, linear inequalities examples, and Application of linear inequations . If this post helped you little bit, then please share it with your friends to benefit them, comment your views on it and also like this post to boost me and to do better, and also follow me on my Blog .We shell meet in next post till then Bye .
If you are a mathematician Don't forget to visit my Mathematics You tube channel ,Mathematics Website and Mathematics Facebook Page , whose links are given below

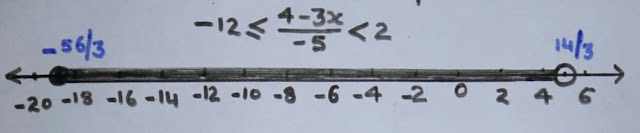











No comments:
Post a Comment
Your valuable suggestions are always acceptable to us for betterment of this website