How to Multiply Two Matrices || Product of Two matrices
How to Multiply Two Matrices , Product of Two matrices
In this post we are going to discuss multiplication of two matrices , i.e. when two matrices can be multiplied with each other or when two matrices are NOT eligible for multiplication, what are the necessary conditions for two matrices to be multiplied.
Before multiplication of two matrices we have to check whether multiplication is possible or not , If it is possible then matrices will be multiplied to each other. Necessary condition for multiplication of two matrices is if " The number of columns in the first matrix is the same as the number of rows in the second matrix ". We must know different types of matrices ,Rows and Column.
Condition for Matrix Multiplication
Before multiplication of two matrices we have to check whether multiplication is possible or not , If it is possible then matrices will be multiplied to each other. Necessary condition for multiplication of two matrices is if " The number of columns in the first matrix is the same as the number of rows in the second matrix ". We must know different types of matrices ,Rows and Column.
Note : The commutation may or may not be possible for multiplication of matrices, That is in some case AB = BA but In general AB is not equal to BA.
Example 1
1. Multiplication of 2 × 3 matrix with 3 × 4 matrix is possible as number of columns in 1st Matrix is equal to numbers of rows in 2nd Matrix and Resultant matrix will be of 2 × 4 order .2. Multiplication of 5 × 1 matrix with 1 × 2 matrix is also possible as it gives 5× 2 matrix as resultant Matrix.
3. Multiplication of 4 ×3 matrix with 2 × 3 matrix is NOT possible. Because red colour numbers 3 and 2 do not match .
How to Multiply Matrices
If condition for matrix multiplication is satisfied, then below is the method of multiplication for two matrices .
Let's take two matrices A and B of 2 × 3 and 3×2 orders respectively. The resultant matrix will be 2 × 2 matrix. we start across the 1st row of the first matrix multiplying down the 1st column of the second matrix, element by element. Then we add the resulting products. Our product will be written in position a11 (top left) of the answer matrix which will be equal to "au+bw+cy".
We shall repeat similar process for the 1st row of the first matrix and the 2nd column of the second matrix. The result will be written in position a12 which will comes out "av+bx+cz".
Now for the 2nd row of the first matrix and the 1st column of the second matrix. The result will be placed in position a21 as "du+ew+fy" .Finally, Multiply the 2nd row of the first matrix and the 2nd column of the second matrix to get the product as "dv+ex+fz" The result is placed in position a22. So the resultant matrix will be written as :--
Let us take one example to Multiply 2×3 and 3×2 Matrices ,The order of resultant matrix will be 2 × 2.
A11 element will be 4×(-3)+1×5+4×6 = -12+5+24 =17
A12 element will be 4×1+1×6+4×4 = 4+6+16 = 26
A21 element will be 2×(-3)-5×5+7×6 = -6-25+42 = 11
A22 element will be 2×1+(-5)×6+7×4 = 2-30+28 = 0
Since the resultant Matrix 2× 2 as follows
A11 element will be 8×(-2)+9×4 = -16 +36 =20
A12 element will be 8×3+9×0 = 24+ 0 = 24
A21 element will be 5×(-2)+(-1)×4 = -10-4 = -14
A22 element will be 5×3+(-1)×0 = 15+0 = 15
so the resultant matrix will be written as
so the resultant matrix will be written as
To find AB
Since Numbers of columns (3) in 1st matrix (Here A Matrix ) is not equal to numbers of Rows (1) in 2nd Matrix (Here Matrix B ). Therefore matrix multiplication is NOT possible in this case.
To Find BA
Since Numbers of columns (3) in 1st matrix (Here B Matrix ) is equal to numbers of Rows (3) in 2nd Matrix (Here A Matrix ). And resultant Matrix shall be 1×3 order . Therefore matrix multiplication is possible in this case and can be calculated in the following manner :-
BA = ( 4*2+3*3+8*3 4*1+3*(-5)+8*2 4*(-7)+3*0+8*(-1) )
BA = ( 8+9+24 4-15+16 -28+0-8 )
BA = ( 41 5 -36 )
Therefore AB is not equal to BA
This video can better demonstrate the multiplication of two matrices .
This video can better demonstrate the multiplication of two matrices .
Important Note
And what about the matrix multiplication of AB and BA of the matrices given below whose order are 4×3 and 3×3 respectively .
Then Matrix Multiplication BA is not possible as the numbers of columns(3) in matrix B is not equal to the numbers of rows (4) in matrix A .
But If we want to Multiply the matrix A with Matrix B as AB then it is possible as the numbers of columns(3) in A matrix is equal to the numbers of rows(3) in B matrix, so it can be calculated as explained earlier.
It means the order of the matrices play very important role to decide whether matrix multiplication is possible or not. And if possible it is again the order of both the matrices to decide what will be the order of the resultant matrix.
It means the order of the matrices play very important role to decide whether matrix multiplication is possible or not. And if possible it is again the order of both the matrices to decide what will be the order of the resultant matrix.
Therefore in multiplication of matrices of 4×3 and 3×3 .The order of resulting matrix will be 4×3 ,The outer most numbers ( Marked red ).
Very Important
If we have two matrices A and B of order 1×3 and 3×1 respectively , and if we have find their product AB and BA , then
In 1st case where we have to find AB , let us check its multiplication would be possible or not , as number of columns (3) in 1st matrix is equal to numbers of rows (3) in 2nd Matrix , so AB would be possible and order of resulting matrix would be 1×1 and it can be found using matrix multiplication .
And if we have find their product BA , then would it be possible or not ? let us check .....
In 2nd case where we have to find BA , let us check its multiplication would be possible or not , as number of columns (1) in 1st matrix is equal to numbers of rows (1) in 2nd Matrix , so AB would be possible and order of resulting matrix would be 3×3 and it can be found using matrix multiplication .
Read this one also HOW TO UNDERSTAND BINARY OPERATIONS ,RELATIONS AND FUNCTIONS || COMMUTATIVE || ASSOCIATIVE
Conclusion
Conclusion
This post was about multiplication of two Matrices, Eligibility conditions for product of matrices, Thanks for giving your valuable time to this post . If you liked this post,Please share your valuable opinions about this post. See you in next post ,till then Bye.

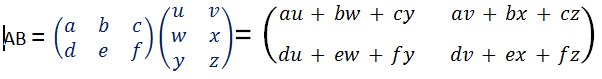












No comments:
Post a Comment
Your valuable suggestions are always acceptable to us for betterment of this website