DIFFERENTIATION OF RAISE TO POWER FUNCTION

Derivative of lnx, derivative of log x^², derivative of e^y,derivative of 2ˣ, Differentiation of raise to power function an easy and short cut manners, differentiation of raise to power function.

Till Date we have learn to differentiate this question by taking log on both sides and then differentiate.

 There is very long process to differentiate this types of functions .

But today we shall learn a different and an easiest method to differentiate such type of functions.

      

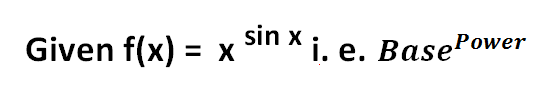
then assume this function as [ log (Base) ]× [ Power ] then use product rule of differentiation and place the given function in front of the result so obtained.

       

Question : Differentiate f(x) = (cos x )^{sin x}

Reduce this problem to product of two function ,1st function will be log of base of given problem and 2nd function will be power of given problem such that 

∴ h(x) = (log cos x) ×(sin x)

then it derivative will be 

 f '(x) = h'(x)

⇒ f '(x) = f(x) [(log cos x) .  (sin x) + sin x  (log cos x)]

Therefore  f '(x) = f(x) [(log cos x) . cos x + sin x (- sin x ) /cos x)]

Therefore  f '(x) = (cos x )^{sin x} [(log cos x) . cos x - sin x .tan x]

Question : How to solve this f(x) = x ^{sin x}  

First of all assume base x as log x as 1st function and power function as 2nd function, then apply Product rule of differentiation, and place f(x) in front of the result so obtained.
{ log x . sin x }= ( log x)( sin x ) + ( sin x )( log x)

= log x . cos x + sin x . (1/x)                            
                     
Now put f(x) in front of this result and that will be derivative of the f(x).
Hence f ' (x) = x ^{sin x} { log x . cos x + sin x . (1/x) }

Question : Differentiate w.r.t. 'x'

 f(x) = cos x ^{sin x} + (sin x) ^x 

Let  f(x) = g(x) + h(x)
Then   f '(x) =g'(x) + h'(x)
Just place cos x ^{sin x}  in front of derivative of {(log cos x) . (sin x) } + place  (sin x) ^x  in front of derivative of { ( log sin x) . ( x) },

So Answer will be

                   

Similarly derivative of h(x) = (sin x) ^x    in one step can also be written as
h '(x) = (sin x) ^x [ log sin x × 1+ x . cos x/sin x ]

Question : Differentiate f(x) = e ^{sin x} 

then using short cut method, 

f '(x) = e ^{sin x}  [ log e . {sin x} + sin x {log  e}]

f '(x) = e ^{sin x}  [ log e × cos x ] ,

f '(x) = cos x .e ^{sin x}   

Because derivative of log e is zero and log e is equal to one

Question : Differentiate f (x) = a ^{sin x} 

If f (x) = a ^{sin x} 

then using short cut method , 

f '(x) =a ^{sin x} [ log a . {sin x} + sin x {log  a}]

f '(x) = a ^{sin x} [ log a . cos x ] ,

Because derivative of log a is zero 

Question : Differentiate f (x) = x ^{sin x + cos x} 

If f (x) = x ^{sin x + cos x} 

then using short cut method , 

f '(x) = x ^{sin x + cos x} [ log x .{sin x + cos x } + {sin x + cos x }{log x}]

f '(x) = x ^{sin x + cos x} [ log x  . {cos x - sin x} + {sin x+cos x }.{1/x} ] 

One more shortcut for differentiation you can use

            

 

Differentiation of Trigonometric Functions

S N	f(x)	f '(x)
1	sin x	cos x
2	cos x	-sin x
3	tan x	sec²x
4	cot x	-cosec²x
5	sec x	sec x tan x
6	cosec x	-cosec x cot x

   

Conclusion

Thanks for devoting your valuable time for this post  differentiation of raise to power function,derivative of lnx, derivative of lnx²,derivative of e^y, derivative of 2ˣ, implicit function differentiation, derivative of logarithmaetic functions of my blog . If you liked this this blog/post,  Do Follow me on my blog and share this post with your friends . We shall meet again   in next post with solutions of most interesting and mind blowing mathematics problems ,till then Good Bye.

PDF

Read More